
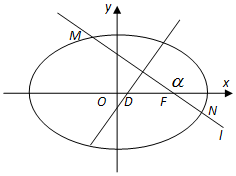
 已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.
已知椭圆E的方程为$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0),E上动点P到右焦点F距离的最大值为3,且离心率e=$\frac{1}{2}$.分析 (Ⅰ)由根据离心率公式及a+c=3,列方程组,即可求得a和c的值,则b2=a2-c2=3,即可求得b的值,求得椭圆方程;
(Ⅱ)由直线l的斜率存在,将直线方程代入椭圆方程,利用弦长公式及三角形的性质,分别求得|FD|,|MN|.即可求得$|DF|=\frac{1}{4}|MN|$.则存在$λ=\frac{1}{4}$,使得|FD|=λ|MN|.
解答 解(Ⅰ)由已知得$\left\{\begin{array}{l}a+c=3\\ \frac{c}{a}=\frac{1}{2}\end{array}\right.$,…(2分)
解得:$\left\{\begin{array}{l}a=2\\ c=1\end{array}\right.$,则b2=a2-c2=3,…(4分)
∴椭圆E的方程为;$\frac{x^2}{4}+\frac{y^2}{3}=1$.…(5分)
(Ⅱ)由(Ⅰ)知椭圆E的右焦点F坐标为(1,0),
∵线段MN垂直平分线交x轴于一点D,∴直线l的斜率存在,
设直线l的方程为y=k(x-1),
(1)当k=0时,|MN|=2a=4,|FD|=c=1,取$λ=\frac{1}{4}$,$|FD|=\frac{1}{4}|MN|$;…(7分)
(2)当k≠0时,设G为线段MN的中点,且M(x1,y1),N(x2,y2),G(x0,y0),
设α为直线l的倾斜角,则$|DF|=\frac{|FG|}{|cosα|}=|FG|\sqrt{1+{{tan}^2}α}=|FG|\sqrt{1+{k^2}}$=$\sqrt{{{({x_0}-1)}^2}+y_0^2}•\sqrt{1+{k^2}}=\sqrt{(1+{k^2}){{({x_0}-1)}^2}}•\sqrt{1+{k^2}}=|{x_0}-1|(1+{k^2})$①…(9分)
$|MN|=\sqrt{(1+{k^2}){{({x_1}-{x_2})}^2}}=\sqrt{(1+{k^2})[{{({x_1}+{x_2})}^2}-4{x_1}{x_2}]}$②…(11分)
由$\left\{\begin{array}{l}y=k(x-1)\\ \frac{x^2}{4}+\frac{y^2}{3}=1\end{array}\right.$得,(3+4k2)x2-8k2x+4k2-12=0,
∴${x_1}+{x_2}=\frac{{8{k^2}}}{{3+4{k^2}}}$、${x_1}•{x_2}=\frac{{4{k^2}-12}}{{3+4{k^2}}}$、${x_0}=\frac{{{x_1}+{x_2}}}{2}=\frac{{4{k^2}}}{{3+4{k^2}}}$…(13分)
代入①②两式并整理得:$|DF|=\frac{{3(1+{k^2})}}{{3+4{k^2}}}$,$|MN|=\frac{{12(1+{k^2})}}{{3+4{k^2}}}$,…(14分)
则$|DF|=\frac{1}{4}|MN|$.
∴存在$λ=\frac{1}{4}$,使得|FD|=λ|MN|.…(16分)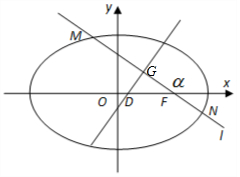
点评 本题考查椭圆的标准方程及简单几何性质,直线与椭圆的位置关系,考查韦达定理,弦长公式的应用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$尺 | B. | $\frac{18}{29}$尺 | C. | $\frac{16}{29}$尺 | D. | $\frac{16}{31}$尺 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 20名学生某次数学成绩(单位:分)的频率分布直方图如图:
20名学生某次数学成绩(单位:分)的频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{7}$ | B. | $\frac{6π}{7}$ | C. | $\frac{8π}{7}$ | D. | $\frac{13π}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3+$\sqrt{5}$ | B. | 5+$\sqrt{5}$ | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )
如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )| A. | “向量的加减法”中“运算法则”的下位 | |
| B. | “向量的加减法”中“运算律”的下位 | |
| C. | “向量的数乘”中“运算法则”的下位 | |
| D. | “向量的数乘”中“运算律”的下位 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
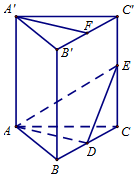 如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:
如图,在直三棱柱ABC-A'B'C'中,AB=AC,D、E分别是棱BC、CC'上的点(点D不同于点C),且AD⊥BC,F为B'C'的中点.求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com