
分析 由函数零点的判定定理列出不等式组,求得实数m的取值范围.
解答 解:由题意可知:二次函数f(x)=7x2-(m+13)x-m-2(m∈R)的两个零点
分别在区间(0,1)和(1,2),
$\left\{\begin{array}{l}{f(0)>0}\\{f(1)<0}\\{f(2)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{-m-2>0}\\{-2m-8<0}\\{-3m>0}\end{array}\right.$,解得:-4<m<-2,
∴实数m的取值范围(-4,-2),
故答案为:(-4,-2).
点评 本题考查一元二次函数零点的判定,考查不等式的解法,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
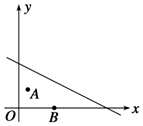 如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?
如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.
如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com