
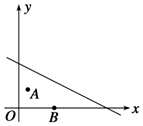
 如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方?
如图所示,某县相邻两镇在一平面直角坐标系下的坐标为A(1,2),B(4,0),一条河所在的直线方程为l:x+2y-10=0,若在河边l上建一座供水站P,使之到A,B两镇的管道最省,那么供水站P应建在什么地方? 分析 根据两点间的距离公式以及点的对称性,建立方程组关系进行求解即可.
解答 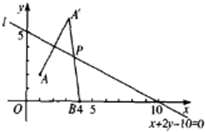 解:过A作直线l的对称点A′,连A′B交l于P,
解:过A作直线l的对称点A′,连A′B交l于P,
∵|AP′|+|P′B|=|A′P′|+|BP′|>|A′B|,
∴P点即为所求.
设A′(a,b),则$\left\{\begin{array}{l}{\frac{a+1}{2}+2•\frac{b+2}{2}-10=0}\\{\frac{b-2}{a-1}•(-\frac{1}{2})=-1}\end{array}\right.$,
即$\left\{\begin{array}{l}{a+2b=15}\\{b=2a}\end{array}\right.$,解得a=3,b=6,
即A′(3,6),
∴直线A′B的方程为$\frac{y-0}{6-0}=\frac{x-4}{3-4}$,即6x+y-24=0,
由$\left\{\begin{array}{l}{6x+y-24=0}\\{x+2y-10=0}\end{array}\right.$,解得x=$\frac{38}{11}$,y=$\frac{36}{11}$,
即P($\frac{38}{11}$,$\frac{36}{11}$),
故供水站P应建在P($\frac{38}{11}$,$\frac{36}{11}$),才能使管道最省.
点评 本题主要考查直线对称性的应用,以及直线交点坐标的求解,利用数形结合是解决本题的关键,是中档题.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:解答题
| P(x2≥k) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )
如图是“向量的线性运算”知识结构图,如果要加入“三角形法则”和“平行四边形法则”,应该放在( )| A. | “向量的加减法”中“运算法则”的下位 | |
| B. | “向量的加减法”中“运算律”的下位 | |
| C. | “向量的数乘”中“运算法则”的下位 | |
| D. | “向量的数乘”中“运算律”的下位 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{5}$ | B. | $\frac{3}{4}$ | C. | $\frac{{\sqrt{34}}}{3}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com