
| 年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
| 年份代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人均纯收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
分析 (1)由所给数据计算得平均数$\overline{t}$、$\overline{y}$,求出回归系数$\widehat{b}$、$\widehat{a}$,即可写出回归直线方程;
(2)根据回归系数$\stackrel{∧}{b}$=0.5>0,判断该地区农村居民家庭人均纯收入逐年增加;将2015年的年份代号t=9代入回归方程计算$\stackrel{∧}{y}$的值即可.
解答 解:(1)由所给数据计算得$\overline{t}$=$\frac{1}{7}$(1+2+3+4+5+6+7)=4,
$\overline{y}$=$\frac{1}{7}$(2.9+3.3+3.6+4.4+4.8+5.2+5.9)=4.3,
计算回归系数
$\widehat{b}$=$\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{{x_i}^2-n(\overline x{)^2}}}}$
=$\frac{(1×2.9+2×3.3+…+7×5.9)-7×4×4.3}{{(1}^{2}+{2}^{2}+…{+7}^{2})-7{×4}^{2}}$=0.5,
$\widehat{a}$=$\overline y$-$\widehat{b}$$\overline x$=4.3-0.5×4=2.3,
所求回归方程为$\stackrel{∧}{y}$=0.5t+2.3;…(6分)
(2)由(1)知,$\stackrel{∧}{b}$=0.5>0,
故2007年至2013年该地区农村居民家庭人均纯收入逐年增加,平均每年增加0.5千元,…(8分)
将2015年的年份代号t=9代入(1)中的回归方程,得$\stackrel{∧}{y}$=0.5×9+2.3=6.8;…(11分)
故预测该地区2015年农村居民家庭人均纯收人为6.8千元.…(12分)
点评 本题考查了线性回归方程的求法与应用问题,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
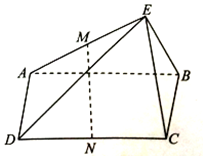 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{5}{2}$,-$\frac{7}{2}$) | B. | ($\frac{5}{2}$,$\frac{7}{2}$) | C. | ($\frac{3}{2}$,-$\frac{7}{2}$) | D. | ($\frac{3}{2}$,$\frac{7}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2e | B. | e | C. | e2 | D. | 2e2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
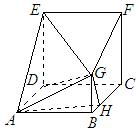 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com