
分析 (1)${a_1}=\frac{5}{3},{a_2}=\frac{7}{3}$,且${a_{n+2}}=\frac{5}{3}{a_{n+1}}-\frac{2}{3}{a_n}\begin{array}{l},{n∈{N^*}}\end{array}$.可得a3=$\frac{5}{3}{a}_{2}-\frac{2}{3}{a}_{1}$.同理可得a4.
(2)由${a_{n+2}}=\frac{5}{3}{a_{n+1}}-\frac{2}{3}{a_n}\begin{array}{l},{n∈{N^*}}\end{array}$.可得:an+2-an+1=$\frac{2}{3}$(an+1-an),a2-a1=$\frac{2}{3}$.利用等比数列的通项公式可得:an+1-an,再利用an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1即可得出.
(3)数列{bn}的前n项和${S_n}=\frac{1}{3}{n^2}$,n≥2时,bn=Sn-Sn-1.n=1时,a1=S1=$\frac{1}{3}$,上式也成立.可得bn=$\frac{2n-1}{3}$.anbn=$\frac{11}{9}$×(2n-1)-(2n-1)×$(\frac{2}{3})^{n}$.设{(2n-1)×$(\frac{2}{3})^{n}$}的前n项和为An,利用错位相减法即可得出.
解答 解:(1)∵${a_1}=\frac{5}{3},{a_2}=\frac{7}{3}$,且${a_{n+2}}=\frac{5}{3}{a_{n+1}}-\frac{2}{3}{a_n}\begin{array}{l},{n∈{N^*}}\end{array}$.
∴a3=$\frac{5}{3}{a}_{2}-\frac{2}{3}{a}_{1}$=$\frac{25}{3}$.
a4=$\frac{5}{3}×\frac{25}{3}-\frac{2}{3}×\frac{7}{3}$=37.
(2)${a_1}=\frac{5}{3},{a_2}=\frac{7}{3}$,且${a_{n+2}}=\frac{5}{3}{a_{n+1}}-\frac{2}{3}{a_n}\begin{array}{l},{n∈{N^*}}\end{array}$.
由${a_{n+2}}=\frac{5}{3}{a_{n+1}}-\frac{2}{3}{a_n}\begin{array}{l},{n∈{N^*}}\end{array}$.
可得:an+2-an+1=$\frac{2}{3}$(an+1-an),a2-a1=$\frac{2}{3}$.
∴数列{an+1-an}是等比数列,首项与公比都为$\frac{2}{3}$.
∴an+1-an=$(\frac{2}{3})^{n}$,
∴an=(an-an-1)+(an-1-an-2)+…+(a2-a1)+a1
=$(\frac{2}{3})^{n-1}+(\frac{2}{3})^{n-2}$+…+$\frac{2}{3}$+$\frac{5}{3}$
=$\frac{1-(\frac{2}{3})^{n}}{1-\frac{2}{3}}$+$\frac{2}{3}$=$\frac{11}{3}$-$2×(\frac{2}{3})^{n-1}$.
(3)数列{bn}的前n项和${S_n}=\frac{1}{3}{n^2}$,
∴n≥2时,bn=Sn-Sn-1=$\frac{1}{3}{n}^{2}-\frac{1}{3}(n-1)^{2}$=$\frac{2n-1}{3}$.
n=1时,b1=S1=$\frac{1}{3}$,上式也成立.
∴bn=$\frac{2n-1}{3}$.
anbn=$\frac{11}{9}$×(2n-1)-(2n-1)×$(\frac{2}{3})^{n}$.
设{(2n-1)×$(\frac{2}{3})^{n}$}的前n项和为An,
则An=$\frac{2}{3}+3×(\frac{2}{3})^{2}$+5×$(\frac{2}{3})^{3}$+…+(2n-1)×$(\frac{2}{3})^{n}$.
$\frac{2}{3}{A}_{n}$=$(\frac{2}{3})^{2}$+$3×(\frac{2}{3})^{3}$+…+(2n-3)×$(\frac{2}{3})^{n}$+(2n-1)×$(\frac{2}{3})^{n+1}$,
∴$\frac{1}{3}{A}_{n}$=$\frac{2}{3}$+2×$[(\frac{2}{3})^{2}+(\frac{2}{3})^{3}$+…+$(\frac{2}{3})^{n}]$-(2n-1)×$(\frac{2}{3})^{n+1}$=$\frac{2}{3}$+2×$\frac{\frac{4}{9}[1-(\frac{2}{3})^{n-1}]}{1-\frac{2}{3}}$(2n-1)×$(\frac{2}{3})^{n+1}$,
可得An=10-(6n+15)×$(\frac{2}{3})^{n+1}$.
∴数列{anbn}的前n项和Tn=$\frac{11}{9}×\frac{n(1+2n-1)}{2}$-10+(6n+15)×$(\frac{2}{3})^{n+1}$
=$\frac{11{n}^{2}}{9}$-10+(6n+15)×$(\frac{2}{3})^{n+1}$.
点评 本题考查了等差数列与等比数列的通项公式及其求和公式、数列递推关系、错位相减法,考查了推理能力与计算能力,属于中档题.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
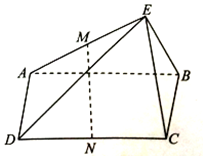 如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:
如图,在四棱锥E-ABCD中,四边形ABCD为矩形,BC⊥EB,EA⊥EB,M,N分别为AE,CD的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{9}{16}$ | C. | $\frac{11}{16}$ | D. | $\frac{13}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2e | B. | e | C. | e2 | D. | 2e2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com