
分析 由在△ABC的中位线上任取一点P,则△PBC的面积等于$\frac{s}{2}$,即满足条件的点P构成的区域,再根据面积比,得到结果.
解答 解:记事件A={△PBC的面积小于$\frac{s}{2}$},
基本事件空间是三角形ABC的面积,(如图)
事件A的几何度量为图中阴影部分的面积(DE是三角形的中位线),
因为阴影部分的面积是整个三角形面积的$\frac{3}{4}$,
所以P(A)=$\frac{3}{4}$.
故答案为:$\frac{3}{4}$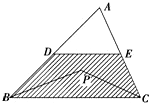
点评 本题考查了几何概型,解答此题的关键在于明确测度比是面积比.对于几何概型常见的测度是长度之比,面积之比,体积之比,角度之比,要根据题意合理的判断和选择是哪一种测度进行求解.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({-\frac{1}{4},0})$ | B. | $({-\frac{1}{4},0}]$ | C. | $[{-\frac{1}{2},1}]$ | D. | $[{-\frac{1}{2},1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{4}{5}i$ | B. | $-\frac{4}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{4}{5}i$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com