
分析 (1)利用f(x)在x=1时取极值,则求出f′(x)得到f′(1)=0,解出求出a即可.
(2)利用函数的导数,判断函数的单调性求解函数的极值即可.
解答 解:(1)∵f′(x)=3x2+6ax-9,f(x)在x=1时取得极值,
∴f′(1)=3+6a-9=0
∴a=1.
(2)由(1)可得f′(x)=3x2+6x-9=3(x-1)(x+3).
函数的极值点为x=1,x=-3,
当x<-3,或x>1时,函数是增函数,x∈(-3,1)时,函数是减函数,
x=-3函数取得极大值,极大值为:f(-3)=32,
x=1时,函数取得极小值,极小值为:f(1)=0.
点评 本题考查学生利用导数研究函数极值的能力,考查学生的计算能力,是中档题.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄(单位:岁) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 3 | 10 | 12 | 7 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 赞成 | |||
| 不赞成 | |||
| 合计 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
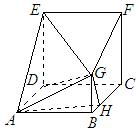 在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH
在多面体ABCDEFG中,四边形ABCD与CDEF是边长均为a的正方形,CF⊥平面ABCD,BG⊥平面ABCD,H是BC上一点,且AB=2BG=4BH 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 2008 | C. | 2017 | D. | 4017 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com