
分析 (Ⅰ)求出函数的导数,计算f(1),f′(1),求出切线方程即可;
(Ⅱ)确定函数f(x)的定义域,求导函数,利用极值的运用,建立方程,结合韦达定理,即可求f(m)+f(n)的取值范围;
(Ⅲ)设t=$\frac{n}{m}$(t>1),确定t的范围,表示出f(n)-f(m),构造新函数,利用导数法确定函数的单调性,即可求得结论.
解答 解:(Ⅰ)a=1时,f(x)=lnx+$\frac{1}{2}$x2-3x,f′(x)=$\frac{1}{x}$+x-3,
f(1)=-$\frac{5}{2}$,f′(1)=-1,
故切线方程是:y+$\frac{5}{2}$=-(x-1),
即2x+2y+3=0;
(Ⅱ)函数f(x)的定义域为(0,+∞),
f′(x)=$\frac{1}{x}$+x-(a+2)=$\frac{{x}^{2}-(a+2)x+1}{x}$,
依题意,方程x2-(a+2)x+1=0有两个不等的正根m,n(其中m<n).
故 $\left\{\begin{array}{l}{{(a+2)}^{2}-4>0}\\{a+2>0}\end{array}\right.$,∴a>0,
并且m+n=a+2,mn=1.
∴f(m)+f(n)=lnmn+$\frac{1}{2}$(m2+n2)-(a+2)(m+n)
=$\frac{1}{2}$[(m+n)2-2mn]-(a+2)(m+n)=-$\frac{1}{2}$(a+2)2-1<-3,
故f(m)+f(n)的取值范围是(-∞,-3). …(7分)
(Ⅲ)当a≥$\sqrt{e}$+$\frac{1}{\sqrt{e}}$-2时,(a+2)2≥e+$\frac{1}{e}$+2.
若设t=$\frac{n}{m}$(t>1),则(a+2)2=(m+n)2=$\frac{{(m+n)}^{2}}{mn}$=t+$\frac{1}{t}$+2≥e+$\frac{1}{e}$+2.
于是有t+$\frac{1}{t}$≥e+$\frac{1}{e}$,∴(t-e)(1-$\frac{1}{te}$)≥0,∴t≥e,
∴f(n)-f(m)
=ln$\frac{n}{m}$+$\frac{1}{2}$(n2-m2)-(a+2)(n-m)
=ln$\frac{n}{m}$+$\frac{1}{2}$(n2-m2)-(n+m)(n-m)
=ln$\frac{n}{m}$-$\frac{1}{2}$(n2-m2)
=ln$\frac{n}{m}$-$\frac{1}{2}$$(\frac{{{n}^{2}-m}^{2}}{mn})$
=ln$\frac{n}{m}$-$\frac{1}{2}$($\frac{n}{m}$-$\frac{m}{n}$)
=lnt-$\frac{1}{2}$(t-$\frac{1}{t}$),
构造函数g(t)=lnt-$\frac{1}{2}$(t-$\frac{1}{t}$)(其中t≥e),
则g′(t)=$\frac{1}{t}$-$\frac{1}{2}$(1+$\frac{1}{{t}^{2}}$)=-$\frac{{(t-1)}^{2}}{{2t}^{2}}$<0.
所以g(t)在[e,+∞)上单调递减,
g(t)≤g(e)=1-$\frac{e}{2}$+$\frac{1}{2e}$,
故f(n)-f(m)的最大值是1-$\frac{e}{2}$+$\frac{1}{2e}$.
点评 本题考查导数知识的运用,考查函数的极值与最值,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bf(lna)<af(lnb) | B. | bf(lna)=af(lnb) | ||
| C. | bf(lna)>af(lnb) | D. | bf(lna)与af(lnb)的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a,b,c都大于0 | B. | a,b,c中至少有一个大于0 | ||
| C. | a,b,c都小于0 | D. | a,b,c中至多有一个大于0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
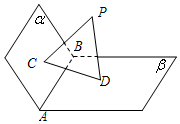 如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.
如图,已知平面α,β,且α∩β=AB,PC⊥α,PD⊥β,C,D是垂足.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 60°或120° | B. | 30°或150° | C. | 60° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com