
分析 (I)(1)对任意α,β∈R,都有g(αβ)=αg(β)+βg(α),且$g({\frac{1}{2}})=1$;可得:${a_{n+1}}=g({\frac{1}{{{2^{n+1}}}}})=g({\frac{1}{2}•\frac{1}{2^n}})=\frac{1}{2}g({\frac{1}{2^n}})+\frac{1}{2^n}g({\frac{1}{2}})=\frac{1}{2}g({\frac{1}{2^n}})+\frac{1}{2^n}$,又数列{an}满足${a_n}=g({\frac{1}{2^n}})$.代入即可证明.
(2)由(1)知:{2nan}是首项和公差均为2的等差数列,故${2^n}{a_n}=2n⇒{a_n}=n•(\frac{1}{2}{)^{n-1}}$.利用错位相减法、等比数列的求和公式即可得出.
(II))由题知:${b_{n+1}}=\frac{{2016{b_n}+2}}{{{b_n}+2017}}$,b1=2.代入变形$⇒\frac{{{b_{n+1}}-1}}{{{b_{n+1}}+2}}=\frac{2015}{2018}•\frac{{{b_n}-1}}{{{b_n}+2}}$.即可证明$\left\{{\frac{{{b_n}-1}}{{{b_n}+2}}}\right\}$是以$\frac{{{b_1}-1}}{{{b_1}+2}}=\frac{1}{4}$为首项,$\frac{2015}{2018}$为公比的等比数列.
解答 解:(Ⅰ)(1)由题知${a_1}=g({\frac{1}{2}})=1$,且${a_{n+1}}=g({\frac{1}{{{2^{n+1}}}}})=g({\frac{1}{2}•\frac{1}{2^n}})=\frac{1}{2}g({\frac{1}{2^n}})+\frac{1}{2^n}g({\frac{1}{2}})=\frac{1}{2}g({\frac{1}{2^n}})+\frac{1}{2^n}$
$⇒{a_{n+1}}=\frac{1}{2}{a_n}+\frac{1}{2^n}$$⇒{2^{n+1}}{a_{n+1}}={2^n}{a_n}+2$.
∴f(x)=x+2是数列{2nan}的母函数;…3分
(2)由(1)知:{2nan}是首项和公差均为2的等差数列,故${2^n}{a_n}=2n⇒{a_n}=n•(\frac{1}{2}{)^{n-1}}$.
∴${S_n}=1+2•(\frac{1}{2}{)^1}+3•(\frac{1}{2}{)^2}+4•{(\frac{1}{2})^3}+…+n•{(\frac{1}{2})^{n-1}}$①
∴$\frac{1}{2}{S_n}=,\frac{1}{2}+2•{(\frac{1}{2})^2},+3•(\frac{1}{2}{)^3}+4•{(\frac{1}{2})^4}+…+n•{(\frac{1}{2})^n}$②
两式相减得:$\frac{1}{2}{S_n}=1+\frac{1}{2}+(\frac{1}{2}{)^2}+{(\frac{1}{2})^3}+…+{(\frac{1}{2})^{n-1}}-n•{(\frac{1}{2})^n}=\frac{{1-\frac{1}{2^n}}}{{1-\frac{1}{2}}}-\frac{n}{2^n}$.
Sn=$2-\frac{n+2}{2^n}$,∴${S_n}=4-\frac{n+2}{{{2^{n-1}}}}$…6分
(Ⅱ)由题知:${b_{n+1}}=\frac{{2016{b_n}+2}}{{{b_n}+2017}}$,b1=2.
∴${b_{n+1}}-1=\frac{{2015({{b_n}-1})}}{{{b_n}+2017}},{b_{n+1}}+2=\frac{{2018({{b_n}+2})}}{{{b_n}+2017}}$$⇒\frac{{{b_{n+1}}-1}}{{{b_{n+1}}+2}}=\frac{2015}{2018}•\frac{{{b_n}-1}}{{{b_n}+2}}$.
从而$\left\{{\frac{{{b_n}-1}}{{{b_n}+2}}}\right\}$是以$\frac{{{b_1}-1}}{{{b_1}+2}}=\frac{1}{4}$为首项,$\frac{2015}{2018}$为公比的等比数列,∴$\frac{{{b_n}-1}}{{{b_n}+2}}=\frac{1}{4}(\frac{2015}{2018}{)^{n-1}}$…8分
又$0.99<\frac{2015}{2018}<0.999$$\begin{array}{l}\\⇒\frac{1}{4}×{0.99^{n-1}}<\frac{{{b_n}-1}}{{{b_n}+2}}=\frac{1}{4}(\frac{2015}{2018}{)^{n-1}}<\frac{1}{4}×{0.999^{n-1}}({n≥2})\end{array}$,
故当n≥2时$\frac{1}{4}\sum_{i=1}^n{{{0.99}^{i-1}}}<{T_n}<\frac{1}{4}\sum_{i=1}^n{{{0.999}^{i-1}}}$$⇒\frac{1}{4}•\frac{{1-{{0.99}^n}}}{1-0.99}<{T_n}<\frac{1}{4}•\frac{{1-{{0.999}^n}}}{1-0.999}$
⇒$25({1-{{0.99}^n}})<{T_n}<250({1-{{0.999}^n}})({n≥2})$…12分
点评 本题考查了数列递推关系、等差数列与等比数列的通项公式与求和公式、错位相减法,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
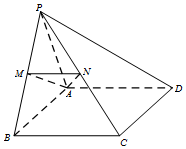 在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.
在四棱锥P-ABCD中,△PAB为正三角形,四边形ABCD为矩形,平面PAB⊥平面ABCD,AB=2AD,M、N分别为PB、PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com