
分析 (Ⅰ)根据题中数据,通过2×2的列联表方法,建立即可;
(Ⅱ)求出K2,然后判断即可.
解答 解:(Ⅰ)
| 患色盲 | 不患色盲 | 总计 | |
| 男 | 38 | 442 | 480 |
| 女 | 6 | 514 | 520 |
| 总计 | 44 | 956 | 1000 |
点评 本题考查独立检验思想方法应用,联列表的求法,考查转化思想以及计算能力.


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016×2017 | B. | 20172 | C. | 2017×2018 | D. | 2018×2019 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
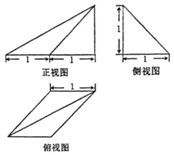
| A. | $\frac{1}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{27}{2}$ | B. | 27 | C. | $27\sqrt{2}$ | D. | $27\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com