
分析 (1)先求出基本事件总数N=6×6=36,由关于x的方程x2+mx+n2=0有两个不等实根,得△=m2-4n2>0,由此利用列举法能求出关于x的方程x2+mx+n2=0有两个不等实根的概率.
(2)利用列举法求出实数$\frac{m}{n}$不是整数包含的基本事件的个数,由此能求出实数$\frac{m}{n}$不是整数的概率.
解答 解:(1)m,n分别表示将一枚质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6,先后抛掷两次时第一次、第二次的点数,
基本事件总数N=6×6=36,
∵关于x的方程x2+mx+n2=0有两个不等实根,
∴△=m2-4n2>0,
∴关于x的方程x2+mx+n2=0有两个不等实根包含的基本事件有:
(3,1),(4,1),(5,1),(5,2),(6,1),(6,2),共6个,
∴关于x的方程x2+mx+n2=0有两个不等实根的概率${p}_{1}=\frac{6}{36}$=$\frac{1}{6}$.
(2)实数$\frac{m}{n}$不是整数包含的基本事件(m,n)有:
(1,2),(1,3),(1,4),(1,5),(1,6),(2,3),(2,4),(2,5),(2,6),
(3,2),(3,4),(3,5),(3,6),(4,3),(4,5),(4,6),(5,2),(5,3),(5,4),(5,6),(6,4),(6,5),共22个,
∴实数$\frac{m}{n}$不是整数的概率p2=$\frac{22}{36}=\frac{11}{18}$.
点评 本题考查古典概型、概率、列举法等基础知识,考查数据处理能力、运算求解能力,考查函数与方程思想、集合思想,是基础题.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{7}{5}$ | C. | $\frac{2}{5}$ | D. | $\frac{8}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | AB边中线所在的直线上 | B. | ∠C平分线所在的直线上 | ||
| C. | 与AB垂直的直线上 | D. | 三角形ABC的外心 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | 1或-1 | C. | 0或±1 | D. | 以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
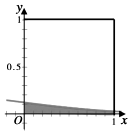 在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )
在如图所示的正方形中随机选择10000个点,则选点落入阴影部分(边界曲线C为正态分布N(-1,1)的密度曲线的一部分)的点的个数的估计值为( )| A. | 906 | B. | 1359 | C. | 2718 | D. | 3413 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com