
| 3 |
| 3 |
| π |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| a2+c2-b2 |
| 2ac |
| 1+3-1 | ||
2•1•
|
| ||
| 2 |
| π |
| 6 |
| π |
| 6 |
| 3 |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 4π |
| 3 |
| π |
| 3 |
| 3 |
| 3 |
| π |
| 3 |
| 3 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| sin2(3π-x) |
| sin(π-x)+cos(π+x) |
| cos(x-2π) |
| 1+tan(π-x) |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
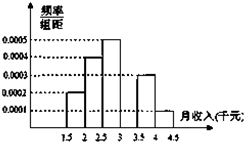 某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是
某调查机构就某单位一千多名职工的月收入进行调查,现从中随机抽出100名,已知抽到的职工的月收入都在[1500,4500)元之间,根据调查结果得出职工的月收入情况残缺的频率分布直方图如图所示,则该单位职工的月收入的平均数大约是查看答案和解析>>
科目:高中数学 来源: 题型:
| A、[32,62] |
| B、(-∞,32]∪[62,+∞) |
| C、(32,62) |
| D、(-∞,32)∪(62,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com