
分析 (1)根据复数对应的点在直线2x-y=0上得到m的方程解之;
(2)将z代入,化简计算.
解答 解:(1)复数z=(m-1)+(m+2)i和复平面内点Z对应,若点Z在直线2x-y=0上,
所以2(m-1)-(m+2)=0
解得m=4.
(2)z=2+i,所以$\frac{{{z^2}-4z+8}}{z-1}$=$\frac{(2+i)^{2}-4(2+i)+8}{2+i-1}$=$\frac{3}{1+i}$=$\frac{3(1-i)}{(1+i)(1-i)}$=$\frac{3-3i}{2}$=$\frac{3}{2}-\frac{3}{2}i$.
点评 本题考查了复数的几何意义以及复数的混合运算;考查学生的运算能力;属于基础题.


 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{4}$ | C. | $2\sqrt{3}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 月收入2000元以下 | 月收入2000元及以上 | 总计 | |
| 高中文化以上 | 10 | 45 | 55 |
| 高中文化及以下 | 20 | 30 | 50 |
| 总计 | 30 | 75 | 105 |
| A. | 1% | B. | 99% | C. | 2.5% | D. | 97.5% |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
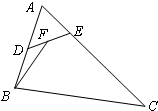 如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )
如图,在△ABC中,已知AB=4,AC=6,∠BAC=60°,点D,E分别在边AB,AC上,且$\overrightarrow{AB}$=2$\overrightarrow{AD}$,$\overrightarrow{AC}$=3$\overrightarrow{AE}$,点F为DE中点,则$\overrightarrow{BF}$•$\overrightarrow{DE}$的值为( )| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}-6x}{(x+3)^{2}}$ | B. | $\frac{{x}^{2}+6x}{x+3}$ | C. | $\frac{{x}^{2}}{(x+3)^{2}}$ | D. | $\frac{{x}^{2}+6x}{(x+3)^{2}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com