
| A. | (0,0) | B. | ($\frac{1}{2}$,1) | C. | (1,$\sqrt{2}$) | D. | (2,2) |
分析 求出焦点坐标和准线方程,把|MF|+|MA|转化为|MA|+|PM|,利用 当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2=2x 解得x值,即得M的坐标.
解答  解:由题意,F($\frac{1}{2}$,0),准线方程为x=-$\frac{1}{2}$,
解:由题意,F($\frac{1}{2}$,0),准线方程为x=-$\frac{1}{2}$,
设M到准线的距离d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,
故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-$\frac{1}{2}$)=$\frac{7}{2}$.
把 y=2代入抛物线y2=2x 得 x=2,故点M的坐标是(2,2),
故选D.
点评 本题考查抛物线的定义和性质应用,解答的关键利用是抛物线定义,体现了转化的数学思想.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{4}$ | B. | $\frac{9}{16}$ | C. | $\frac{9}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
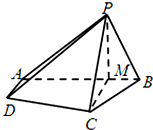 在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.
在四棱锥P-ABCD中,AD∥BC,∠ABC=∠APB=90°,点M是线段AB上的一点,且PM⊥CD,AB=BC=2PB=2AD=4BM.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{7}\;\;,\;\;1}]$ | B. | $[{-1\;\;,\;\;\frac{1}{7}}]$ | ||
| C. | $(-∞\;\;,\;\;-\frac{1}{7}]∪[1\;\;,\;\;+∞)$ | D. | [1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{3}$) | B. | $\sqrt{3}$f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{3}$) | C. | $\sqrt{3}$f($\frac{π}{4}$)<$\sqrt{2}$f($\frac{π}{6}$) | D. | f($\frac{π}{4}$)>$\sqrt{2}$f($\frac{π}{6}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com