
如图,已知双曲线C1: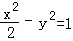 ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“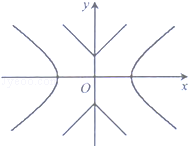
(1)在正确证明C1的左焦点是“C1﹣C2型点“时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1﹣C2型点”;
(3)求证:圆x2+y2= 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”
(1)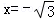 或
或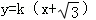 ,其中
,其中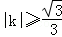 (2)见解析(3)见解析
(2)见解析(3)见解析
解析试题分析:C1的左焦点为(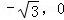 ),写出的直线方程可以是以下形式:
),写出的直线方程可以是以下形式: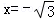 或
或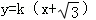 ,其中
,其中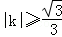 .
.
(2)证明:因为直线y=kx与C2有公共点,
所以方程组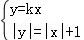 有实数解,因此|kx|=|x|+1,得
有实数解,因此|kx|=|x|+1,得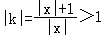 .
.
若原点是“C1﹣C2型点”,则存在过原点的直线与C1、C2都有公共点.
考虑过原点与C2有公共点的直线x=0或y=kx(|k|>1).
显然直线x=0与C1无公共点.
如果直线为y=kx(|k|>1),则由方程组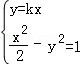 ,得
,得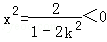 ,矛盾.
,矛盾.
所以直线y=kx(|k|>1)与C1也无公共点.
因此原点不是“C1﹣C2型点”.
(3)证明:记圆O: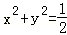 ,取圆O内的一点Q,设有经过Q的直线l与C1,C2都有公共点,显然l不与x轴垂直,
,取圆O内的一点Q,设有经过Q的直线l与C1,C2都有公共点,显然l不与x轴垂直,
故可设l:y=kx+b.
若|k|≤1,由于圆O夹在两组平行线y=x±1与y=﹣x±1之间,因此圆O也夹在直线y=kx±1与y=﹣kx±1之间,
从而过Q且以k为斜率的直线l与C2无公共点,矛盾,所以|k|>1.
因为l与C1由公共点,所以方程组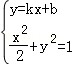 有实数解,
有实数解,
得(1﹣2k2)x2﹣4kbx﹣2b2﹣2=0.
因为|k|>1,所以1﹣2k2≠0,
因此△=(4kb)2﹣4(1﹣2k2)(﹣2b2﹣2)=8(b2+1﹣2k2)≥0,
即b2≥2k2﹣1.
因为圆O的圆心(0,0)到直线l的距离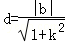 ,
,
所以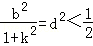 ,从而
,从而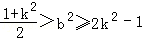 ,得k2<1,与|k|>1矛盾.
,得k2<1,与|k|>1矛盾.
因此,圆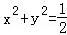 内的点不是“C1﹣C2型点”
内的点不是“C1﹣C2型点”
考点:直线与圆锥曲线的关系;点到直线的距离公式;双曲线的简单性质
点评:本题考查了双曲线的简单几何性质,考查了点到直线的距离公式,考查了直线与圆锥曲线的关系,直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨论、函数与方程、等价转化等数学思想方法.属难题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
在平面直角坐标系中,动点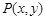 到两条坐标轴的距离之和等于它到点
到两条坐标轴的距离之和等于它到点 的距离,记点
的距离,记点 的轨迹为曲线
的轨迹为曲线 .
.
(I) 给出下列三个结论:
①曲线 关于原点对称;
关于原点对称;
②曲线 关于直线
关于直线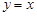 对称;
对称;
③曲线 与
与 轴非负半轴,
轴非负半轴,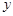 轴非负半轴围成的封闭图形的面积小于
轴非负半轴围成的封闭图形的面积小于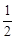 ;
;
其中,所有正确结论的序号是_____;
(Ⅱ)曲线 上的点到原点距离的最小值为______.
上的点到原点距离的最小值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com