
直线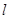 与双曲线C:
与双曲线C: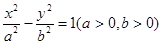 交于
交于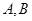 两点,
两点,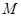 是线段
是线段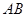 的中 点,若
的中 点,若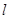 与
与 (
( 是原点)的斜率的乘积等于
是原点)的斜率的乘积等于 ,则此双曲线的离心率为 ___
,则此双曲线的离心率为 ___
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:高中数学 来源: 题型:填空题
如图,已知双曲线C1: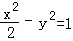 ,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“
,曲线C2:|y|=|x|+1,P是平面内一点,若存在过点P的直线与C1,C2都有公共点,则称P为“C1﹣C2型点“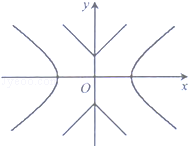
(1)在正确证明C1的左焦点是“C1﹣C2型点“时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线y=kx与C2有公共点,求证|k|>1,进而证明原点不是“C1﹣C2型点”;
(3)求证:圆x2+y2= 内的点都不是“C1﹣C2型点”
内的点都不是“C1﹣C2型点”
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列说法中,正确的有 .
①若点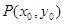 是抛物线
是抛物线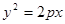 上一点,则该点到抛物线的焦点的距离是
上一点,则该点到抛物线的焦点的距离是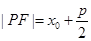 ;
;
②设 、
、 为双曲线
为双曲线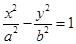 的两个焦点,
的两个焦点,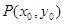 为双曲线上一动点,
为双曲线上一动点,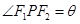 ,则
,则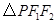 的面积为
的面积为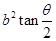 ;
;
③设定圆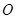 上有一动点
上有一动点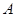 ,圆
,圆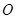 内一定点
内一定点 ,
,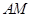 的垂直平分线与半径
的垂直平分线与半径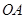 的交点为点
的交点为点 ,则
,则 的轨迹为一椭圆;
的轨迹为一椭圆;
④设抛物线焦点到准线的距离为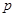 ,过抛物线焦点
,过抛物线焦点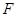 的直线交抛物线于A、B两点,则
的直线交抛物线于A、B两点,则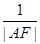 、
、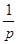 、
、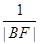 成等差数列.
成等差数列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com