
观察下列等式:
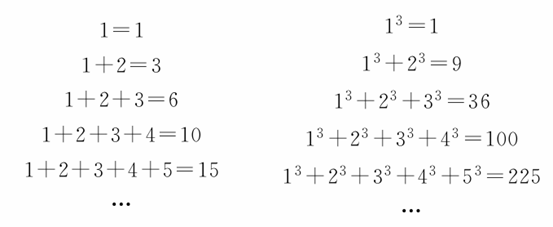

可以推测:13+23+33+…+n3=________(n∈N*,用含n的代数式表示).
科目:高中数学 来源: 题型:
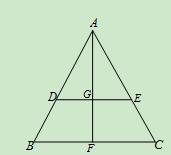
如图1,在边长为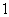 的等边三角形
的等边三角形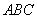 中,
中,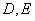 分别是
分别是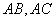 边上的点,
边上的点,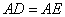 ,
,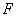 是
是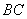 的中点,
的中点,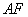 与
与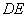 交于点
交于点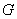 ,将
,将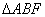 沿
沿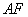 折起,得到如图2所示的三棱锥
折起,得到如图2所示的三棱锥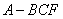 ,其中
,其中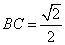 .
.
(1)证明: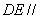 平面
平面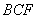 ;(2) 证明:
;(2) 证明: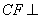 平面
平面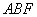 ;
;
(3)当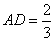 时,求三棱锥
时,求三棱锥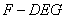 的体积
的体积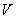 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
为应对金融危机,刺激消费,某市给市民发放面额为100元的旅游消费卷,由抽样调查预计老、中、青三类市民持有这种消费卷到某旅游景点消费额及其概率如下表:
| 200元 | 300元 | 400元 | 500元 | |
| 老年 | 0.4 | 0.3 | 0.2 | 0.1 |
| 中年 | 0.3 | 0.4 | 0.2 | 0.1 |
| 青年 | 0.3 | 0.3 | 0.2 | 0.2 |
某天恰好有持有这种消费卷的老年人、中年人、青年人各一人到该旅游景点,(1)求这三人恰有两人消费额不少于300元的概率;(2)求这三人消费总额大于或等于1300元的概率。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com