练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    现有下列命题：

    ①设a，b为正实数，若a2﹣b2=1，则a﹣b＜1；

    ②设，均为单位向量，若；

    ③数列；

    ④设函数，则关于x的方程f2（x）+2f（x）=0有4个解．

    其中的真命题有　　．（写出所有真命题的编号）．

    【答案】①②③

    【解析】①若a2﹣b2=1，则a2﹣1=b2，

    即（a+1）（a﹣1）=b2，

    ∵a+1＞a﹣1，

    ∴a﹣1＜b，即a﹣b＜1，①正确；

    ②若，则，

    即2+2cosθ＞1，cosθ＞﹣，

    又∵θ∈[0，π]，

    ∴θ∈[0，），②正确；

    ③由an=n（n+4）（）n，

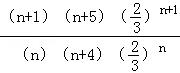    令==≥1，

    则2（n+1）（n+5）≥3n（n+4），

    即n2≤10，所以n＜4，

    即n＜4时，an+1＞an，

    当n≥4时，an+1＜an，

    所以a4最大，故③正确；

    令f2（x）+2f（x）=0，

    则f（x）=0，或f（x）=﹣2，

    ∵，

    ∴当f（x）=0时，

    x=1，或x=0，或x=2，

    当f（x）=﹣2时，x=10.1或x=0.99，

    故方程有5个解，故④错误

    故答案为：①②③

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    设V是已知平面M上所有向量的集合，对于映射f：V→V，a∈V，记a的象为f（a）．若映射f：V→V满足：对所有a、b∈V及任意实数λ，μ都有f（λa+μb）=λf（a）+μf（b），则f称为平面M上的线性变换．现有下列命题：
    ①设f是平面M上的线性变换，a、b∈V，则f（a+b）=f（a）+f（b）；
    ②若e是平面M上的单位向量，对a∈V，设f（a）=a+e，则f是平面M上的线性变换；
    ③对a∈V，设f（a）=-a，则f是平面M上的线性变换；
    ④设f是平面M上的线性变换，a∈V，则对任意实数k均有f（ka）=kf（a）．
    其中的真命题是
     
    （写出所有真命题的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设V是已知平面M上所有向量的集合，对于映射f：V→V，
    a
    ∈V    ，记
    a
    的象为f(
    a
    )    ．若映射f：V→V满足：对所有
    a
    ，
    b
    ∈V    及任意实数λ，μ都有f(λ
    a
    +μ
    b
    )=λf(
    a
    )+μf(
    b
    )    ，则f称为平面M上的线性变换．现有下列命题：
    ①设f是平面M上的线性变换，则f(
    0
    )=
    0

    ②对
    a
    ∈V    设f(
    a
    )=2
    a
    ，则f是平面M上的线性变换；
    ③若
    e
    是平面M上的单位向量，对
    a
    ∈V    设f(
    a
    )=
    a
    -
    e
    ，则f是平面M上的线性变换；
    ④设f是平面M上的线性变换，
    a
    ，
    b
    ∈V    ，若
    a
    ，
    b
    共线，则f(
    a
    )，f(
    b
    )    也共线．
    其中真命题是
     
    （写出所有真命题的序号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    现有下列命题：
    ①设a，b为正实数，若a2-b2=1，则a-b＜1；
    ②已知a＞2b＞0，则a2+
    8
    b(a-2b)
    的最小值为16；
    ③数列{n(n+4)(
    2
    3
    )n}中的最大项是第4项    ；
    ④设函数f(x)=
    lg|x-1|，x≠1
    0，x=1
    ，则关于x的方程f2（x）+2f（x）=0有4个解．
    ⑤若sinx+siny=
    1
    3
    ，则siny-cos2x的最大值是
    4
    3
    ．
    其中的真命题有
    ①②③
    ①②③
    ．（写出所有真命题的编号）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    现有下列命题：
    ①设a，b为正实数，若a2-b2=1，则a-b＜1；
    ②设
    a
    ，
    b
    均为单位向量，若|
    a
    +
    b
    |＞1则θ∈[0，
    2π
    3
    )    ；
    ③数列{n(n+4)(
    2
    3
    )n}中的最大项是第4项    ；
    ④设函数f(x)=
    lg|x-1|，x≠1
    0，x=1
    ，则关于x的方程f2（x）+2f（x）=0有4个解．
    其中的真命题有
    ①②③
    ①②③
    ．（写出所有真命题的编号）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•四川）记[x]为不超过实数x的最大整数，例如，[2]=2，[1.5]=1，[-0.3]=-1．设a为正整数，数列{xn}满足x1=a，xn+1=[
    xn+[
    a
    xn
    ]
    2
    ](n∈N*)    ，现有下列命题：
    ①当a=5时，数列{xn}的前3项依次为5，3，2；
    ②对数列{xn}都存在正整数k，当n≥k时总有xn=xk；
    ③当n≥1时，xn＞
    		a
    -1    ；
    ④对某个正整数k，若xk+1≥xk，则xk=[
    		a
    ]    ．
    其中的真命题有
    ①③④
    ①③④
    ．（写出所有真命题的编号）

    查看答案和解析>>

    同步练习册答案