练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．某市在“国际禁毒日”期间，连续若干天发布了“珍爱生命，远离毒品”的电视公益广告，期望让更多的市民知道毒品的危害性．禁毒志愿者为了了解这则广告的宣传效果，随机抽取了100名年龄阶段在[10，20），[20，30），[30，40），[40，50），[50，60）的市民进行问卷调查，由此得到样本频率分布直方图如图所示．
    （1）从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人，求[50，60）年龄段抽取的人数；
    （2）从（1）中方式得到的5人中在抽取2人作为本次活动的获奖者，求[50，60）年龄段仅1人获奖的概率．

    分析 （1）先分别求出[40，50）年龄段的频率和[50，60）年龄段的频率，由此能求出[50，60）年龄段抽取的人数．
    （2）抽到的5人中[40，50）年龄段的人数为3人，[50，60）年龄段的人数为2人，由此能求出5人中在抽取2人作为本次活动的获奖者，[50，60）年龄段仅1人获奖的概率．

    解答 解：（1）不小于40岁的人中，[40，50）年龄段的频率为0.015×10=0.15，
    [50，60）年龄段的频率为0.010×10=0.1，
    ∴[40，50）年龄段的人数为0.15×100=15，
    [50，60）年龄段的人数为0.1×100=10，
    ∵从不小于40岁的人中按年龄段分层抽样的方法随机抽取5人，
    ∴[50，60）年龄段抽取的人数为：5×$\frac{10}{10+15}$=2人．
    （2）由（1）知抽到的5人中[40，50）年龄段的人数为3人，
    [50，60）年龄段的人数为2人，
    ∴5人中在抽取2人作为本次活动的获奖者，
    [50，60）年龄段仅1人获奖的概率：p=$\frac{{C}_{3}^{1}{C}_{2}^{1}}{{C}_{5}^{2}}$=$\frac{3}{5}$．

    点评 本题考查频数的求法，考查概率的求法，是基础题，解题时要认真审题，注意频率分布直方图的性质的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    15．下列函数中，既不是奇函数，也不是偶函数的是（　　）
    A．f（x）=0B．f（x）=2x+$\frac{1}{2^x}$C．f（x）=sinx+xD．f（x）=lg|x|+x

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    6．已知向量$\overrightarrow a$与$\overrightarrow b$的夹角为θ，定义$\overrightarrow a×\overrightarrow b$为$\overrightarrow a$与$\overrightarrow b$的“向量积”，且$\overrightarrow a×\overrightarrow b$是一个向量，它的长度$|\overrightarrow a×\overrightarrow b|=|{\overrightarrow a}||{\overrightarrow b}|sinθ$，若$\overrightarrow u=（2，0），\overrightarrow u-\overrightarrow v=（1，-\sqrt{3}）$，则|$\overrightarrow u×（\overrightarrow u-\overrightarrow v）$|=（　　）
    A．$4\sqrt{3}$B．$\sqrt{3}$C．6D．$2\sqrt{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

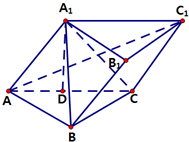    3．在斜三棱柱ABC-A1B1C1中BC⊥CC1，AC=BC=2，A1在底面ABC上的射影恰为AC的中点D．
    （1）证明：BC⊥平面ACC1A1
    （2）若二面角A-A1B-C的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．设α、β、γ满足0＜α＜β＜γ＜2π，若cos（x+α）+cos（x+β）+cos（x+γ）=0对任意实数x均成立，则α-β的值是（　　）
    A．$-\frac{π}{3}$B．$-\frac{2π}{3}$C．$-\frac{4π}{3}$D．$-\frac{2π}{3}$或$-\frac{4π}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    20．已知函数f（x）=ln（x+a）-x，a∈R．
    （1）当a=-1时，求f（x）的单调区间；
    （2）若x≥1时，不等式${e^{f（x）}}+\frac{a}{2}{x^2}＞1$成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．下面为函数y=xsinx+cosx的递增区间的是（　　）
    A．（$\frac{π}{2}$，$\frac{3π}{2}$）B．（π，2π）C．（0，$\frac{π}{2}$）D．（2π，3π）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    4．过抛物线x2=2y上一点A（不与原点O重合）作抛物线的切线m，过A作m的垂线l，若l恰好经过（0，2），则点A的坐标为（$\sqrt{2}$，1）或（-$\sqrt{2}$，1）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．设数列 {an} 的前n项和为Sn（n∈N*），关于数列 {an} 有下列四个命题：
    ①若 {an}既是等差数列又是等比数列，则 an=an+1（n∈N*）；
    ②若  Sn=an2+bn（a，b∈R），则 {an}是等差数列；
    ③若 Sn=1-（-1）n，则 {an}是等比数列；
    ④若 S1=1，S2=2，且 Sn+1-3Sn+2Sn-1=0（n≥2），则数列 {an}是等比数列．
    这些命题中，真命题的序号是①②③．

    查看答案和解析>>

    同步练习册答案