
分析 (1)代入a=-1可知f(x)的解析式,通过求导,分1<x<2、x>2两种情况讨论即可;
(2)一方面通过定义域及x≥1可知a>-1,另一方面通过变形可知只需$a>\frac{{2({e}-1)}}{{{e}+2}}$,进而设$h(x)=\frac{{2({e}-1)}}{{{e}+2}}({{e}^x}x-1)+1-x,x≥1$,只需通过求导证明h(x)在(1,+∞)上单调递增,计算可知aexx-x+1-a>0.结合两方面即得结论.
解答 解:(1)当a=-1,f(x)=ln(x-1)-x,x>1.
$f'(x)=\frac{1}{x-1}-1=\frac{1-x+1}{x-1}=\frac{2-x}{x-1}$.
当1<x<2时,f'(x)>0,f(x)单调递增;
当x>2时,f'(x)<0,f(x)单调递减.
综上,f(x)的单调递增区间为(1,2);单调递减区间为(2,+∞).(4分)
(2)由题意得,x≥1时,x+a>0恒成立,可得a>-1.①
由题意得,不等式$\frac{a}{2}{x^2}+\frac{x+a}{{{{e}^x}}}-1>0$对于任意的x≥1恒成立.
设$g(x)=\frac{a}{2}{x^2}+\frac{x+a}{{{{e}^x}}}-1$,x≥1.则$g'(x)=\frac{{a{{e}^x}x-x+1-a}}{{{{e}^x}}}$.
当a≤0时,$g(2)=2a+\frac{2+a}{{{{e}^2}}}-1=a(2+\frac{1}{{{{e}^2}}})-1+\frac{2}{{{{e}^2}}}<0$,不满足题意;
当a>0时,要使x≥1时,不等式${{e}^{f(x)}}+\frac{a}{2}{x^2}>1$成立,
须$g(1)=\frac{a}{2}+\frac{1+a}{e}-1=a(\frac{1}{2}+\frac{1}{e})-1+\frac{1}{e}>0$,即$a>\frac{{2({e}-1)}}{{{e}+2}}$; (8分)
当$a>\frac{2(e-1)}{e+2}$时,$a{{e}^x}x-x+1-a=a({{e}^x}x-1)+1-x>\frac{{2({e}-1)}}{{{e}+2}}({{e}^x}x-1)+1-x$,
设$h(x)=\frac{{2({e}-1)}}{{{e}+2}}({{e}^x}x-1)+1-x,x≥1$,则$h'(x)=\frac{{2({e}-1)}}{{{e}+2}}{{e}^x}x+\frac{{2({e}-1)}}{{{e}+2}}{{e}^x}-1,x≥1$.
显然h'(x)在(1,+∞)上单调递增,所以$h'(x)>h'(1)=\frac{{4{{e}^2}-5{e}-2}}{{{e}+2}}>0$.
所以h(x)在(1,+∞)上单调递增,$h(x)>h(1)=\frac{{2{{({e}-1)}^2}}}{{{e}+2}}>0$.
即aexx-x+1-a>0.…②
由①②可知$a>\frac{{2({e}-1)}}{{{e}+2}}$时,满足题意.(12分)
点评 本题考查利用导数研究函数的单调性,考查运算求解能力,注意解题方法的积累,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | A、B、D三点共线 | B. | A、B、C三点共线 | C. | B、C、D三点共线 | D. | A、C、D三点共线 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
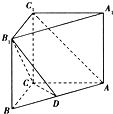 在直三棱柱ABC-A1B1C1中,AC=BC,点D在线段AB上,且平面B1CD⊥平面ABB1A1.
在直三棱柱ABC-A1B1C1中,AC=BC,点D在线段AB上,且平面B1CD⊥平面ABB1A1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$i | B. | $\frac{2}{5}$ | C. | -$\frac{1}{5}$i | D. | -$\frac{1}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.
某市在“国际禁毒日”期间,连续若干天发布了“珍爱生命,远离毒品”的电视公益广告,期望让更多的市民知道毒品的危害性.禁毒志愿者为了了解这则广告的宣传效果,随机抽取了100名年龄阶段在[10,20),[20,30),[30,40),[40,50),[50,60)的市民进行问卷调查,由此得到样本频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{2}{9}$ | D. | $\frac{1}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com