考点:直线与圆锥曲线的综合问题,椭圆的标准方程
专题:综合题,圆锥曲线中的最值与范围问题
分析:(Ⅰ)由椭圆离心率可化简椭圆方程为3x2+4y2=3a2,设椭圆上任意一点P(x0,y0),由两点间距离公式可表示|PQ|为x0的函数,利用二次函数的性质可求得函数的最大值,令其为3可求a;
(Ⅱ)设A(x1,y1),B(x2,y2),当直线AB垂直x轴时,求出M点坐标可判断|PQ|2+2|OM|2是否为定值,由椭圆性质可求|OP|+|OQ|的最大值;
解答:
解:(I)∵椭圆C:
+
=1(a>b>0)的离心率e=
,椭圆上的点到点Q(1,0)的距离的最大值为3,
∴
e==
=
,∴
b2=a2,∴3x
2+4y
2=3a
2,
设椭圆上任意一点P(x
0,y
0),
则
|PQ|==(-a≤x0≤a),
记
f(x0)=,
当a≥4时,|PQ|
max=f(-a)=3,解得a=-4(舍)或a=2(舍);
当0<a<4时,|PQ|
max=f(-a)=3,解得a=-4(舍)或a=2.
∴椭圆C的方程为
+=1.
(Ⅱ)设A(x
1,y
1),B(x
2,y
2),
当直线AB垂直x轴时,由
S△AOB=可得|x
1y
1|=
,
与
+=1联立可求得|x
1|=
,|y
1|=
,
当A(
,
)时,M(
,0),
2|OM|
2=4,而P为动点,Q为定点,则|PQ|
2为变量,
∴|PQ|
2+2|OM|
2不为定值.
由椭圆的性质知,|OP|+|OQ|的最大值为a+c=2+1=3.
点评:该题考查椭圆的方程性质、考查直线与椭圆的位置关系、三角形的面积等知识,考查学生分析解决问题的能力.



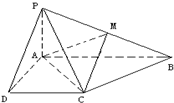 已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=
已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=