
分析 设切点为(${x}_{0},{{x}_{0}}^{3}-2{x}_{0}$),利用导数的几何意义,求得切线的斜率k=f′(x0),利用点斜式写出切线方程,将点(1,m)代入切线方程,可得关于x0的方程有三个不同的解,利用参变量分离可得2$2{{x}_{0}}^{3}-3{{x}_{0}}^{2}=-2-m$,令g(x)=2x3-3x2,利用导数求出g(x)的单调性和极值,则根据y=g(x)与y=-2-m有三个不同的交点,即可得到m的取值范围.
解答 解:设切点为(${x}_{0},{{x}_{0}}^{3}-2{x}_{0}$),
由f(x)=x3-2x,得f′(x)=3x2-2,
∴$f′({x}_{0})=3{{x}_{0}}^{2}-2$.
则切线方程为$y-{{x}_{0}}^{3}+2{x}_{0}=(3{{x}_{0}}^{2}-2)(x-{x}_{0})$.
把(1,m)代入,可得m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$.
∵过点A(1,m)(m≠-2)可作曲线y=f(x)的三条切线,
∴方程m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$有三个不同的根,
令g(x)=2x3-3x2,
∴g′(x)=6x2-6x=0,解得x=0或x=1,
当x<0时,g′(x)>0,当0<x<1时,g′(x)<0,当x>1时,g′(x)>0,
∴g(x)在(-∞,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,
∴当x=0时,g(x)取得极大值g(0)=0,
当x=1时,g(x)取得极小值g(1)=-1,
关于x0的方程m=$-2{{x}_{0}}^{3}+3{{x}_{0}}^{2}-2$有三个不同的根,
等价于y=g(x)与y=-2-m的图象有三个不同的交点,
∴-1<-2-m<0,
∴-2<m<-1,
∴实数m的取值范围为(-2,-1).
故答案为:(-2,-1).
点评 本题考查了利用导数研究曲线上某点切线方程.导数的几何意义即在某点处的导数即该点处切线的斜率,解题时要注意运用切点在曲线上和切点在切线上.运用了转化的数学思想方法,对能力要求较高.属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
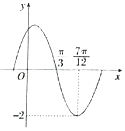 函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )
函数f(x)=Asin(ωx+φ)(A,ω,φ是常数,A>0,ω>0)的部分图象如图所示,则下列结论:①将f(x)的图象向左平移$\frac{π}{6}$个单位,所得到的函数是偶函数:②f(0)=1;③最小正周期为π;④$f(\frac{12π}{11})<f(\frac{14π}{13})$;⑤$f(x)=-f(\frac{5π}{3}-x)$.其中正确的结论有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2,2] | B. | [2,+∞) | C. | [0,+∞) | D. | (-∞,-2]∪[2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 一半径为4m的水轮(如图),水轮圆心O距离水面2m,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计时.
一半径为4m的水轮(如图),水轮圆心O距离水面2m,已知水轮每分钟转动4圈,如果当水轮上点P从水中浮现时(图中点P0)开始计时.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com