
| A. | (-∞,-2)∪(2,+∞) | B. | (-∞,-2)∪(0,2) | C. | (-2,0)∪(0,2) | D. | (-2,0)∪(2,+∞) |
分析 设g(x)=$\frac{f(x)}{x}$,根据函数的单调性和函数的奇偶性求出不等式的解集即可.
解答 解:设g(x)=$\frac{f(x)}{x}$,
∴g′(x)=$\frac{xf′(x)-f(x)}{{x}^{2}}$,
∵当x>0时,有xf′(x)-f(x)>0恒成立,
∴当x>0时,g′(x)>0
∴g(x)在(0,+∞)递增,
∵f(-x)=f(x),
∴g(-x)=$\frac{f(-x)}{-x}$=-g(x),
∴g(x)是奇函数,
∴g(x)在(-∞,0)递增,
∵f(2)=0
∴g(2)=$\frac{f(2)}{2}$=0,
当x>0时,f(x)<0等价于$\frac{f(x)}{x}$<0,
∴g(x)<0=g(2),
∴0<x<2,
当x<0时,f(x)<0等价于$\frac{f(x)}{x}$>0,
∴g(x)>0=g(-2),
∴-2<x<0,
不等式f(x)<0的解集为(-2,0)∪(0,2),
故选:C.
点评 本题主要考察函数奇偶性的应用,考查函数的单调性,是一道中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
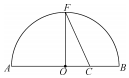 《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )
《几何原本》卷2的几何代数法(以几何方法研究代数问题)成了后世西方数学家处理问题的重要依据,通过这一原理,很多的代数的公理或定理都能够通过图形实现证明,也称之为无字证明.现有如图所示图形,点F在半圆O上,点C在直径AB上,且OF⊥AB,设AC=a,BC=b,则该图形可以完成的无字证明为( )| A. | $\frac{a+b}{2}≥\sqrt{ab}$(a>0,b>0) | B. | a2+b2≥2ab(a>0,b>0) | ||
| C. | $\frac{2ab}{a+b}≤\sqrt{ab}$(a>0,b>0) | D. | $\frac{a+b}{2}≤\sqrt{\frac{{{a^2}+{b^2}}}{2}}$(a>0,b>0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5$\sqrt{13}$ | B. | 5$\sqrt{11}$ | C. | 5$\sqrt{7}$ | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ①或③ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.35 | B. | 0.32 | C. | 0.55 | D. | 0.68 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com