
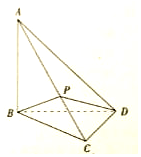
 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )| A. | 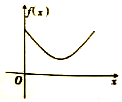 | B. | 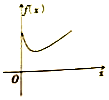 | C. | 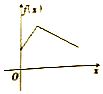 | D. | 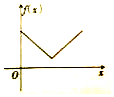 |
分析 利用异面直线之间的距离,求出三角形的面积,即可推出函数的图象.
解答  解:AB⊥平面BCD,且BD⊥CD,设AB=BD=CD=a,
解:AB⊥平面BCD,且BD⊥CD,设AB=BD=CD=a,
过P作PO⊥BC 于O,作ON⊥BD 于N,连接PN,
则PN⊥BD,AC=$\sqrt{3}a$,
设CP的长度为x,$\frac{PO}{AB}=\frac{PC}{AC}$,
PO=$\frac{\sqrt{3}}{3}x$,$\frac{PO}{AB}=\frac{OC}{BC}$,OC=$\frac{\sqrt{2}ax}{\sqrt{3}a-x}$,
ON=a-$\frac{ax}{\sqrt{3}a-x}$.
PN=$\sqrt{(\frac{\sqrt{3}}{3}x)^{2}+(a-\frac{ax}{\sqrt{3}a-x})^{2}}$=$\sqrt{\frac{1}{3}{x}^{2}+{a}^{2}(\frac{\sqrt{3}a-2x}{\sqrt{3}a-x})^{2}}$.
△PBD的面积为f(x)=$\frac{1}{2}a•PN$=$\frac{1}{2}a$$\sqrt{\frac{1}{3}{x}^{2}+{a}^{2}(\frac{\sqrt{3}a-2x}{\sqrt{3}a-x})^{2}}$
=$\frac{1}{2}a$$\sqrt{\frac{1}{3}{x}^{2}+{a}^{2}(1-\frac{x}{\sqrt{3}a-x})^{2}}$.
x$∈[0,\sqrt{3}a]$.
PN由a逐渐减小(由函数的解析式可知函数的图象不是直线变化)然后逐渐增大到a,
函数的图象为:A.
故选:A.
点评 本题考查函数的图象的判断,函数的解析式的求法,考查分析问题解决问题的能力.


 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3022 | B. | -3022 | C. | 2017 | D. | -2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
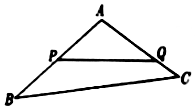 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com