
分析 (Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)求出函数f(x)的导数,设函数F(x)=f(x)-f(-x),求出函数的导数,根据函数的单调性证明即可.
解答 解:(Ⅰ)f(x)=ex+ax的定义域为(-∞,+∞),f′(x)=ex+a,
当a≥0时,f′(x)>0在x∈(-∞,+∞)时成立,
∴f(x)在(-∞,+∞)上单调递增,f(x)无极值;
当a<0时,f′(x)=ex+a=0解得x=ln(-a),
∴f(x)在(-∞,ln(-a))上单调递减,f(x)在(ln(-a),+∞)上单调递增,
f(x)有极小值$aln({-a})-a=aln({\frac{-a}{e}})$.
(Ⅱ)证明:当a=-1时,f(x)=ex-x的定义域为(-∞,+∞),f′(x)=ex-1,
由f′(x)=ex-1=0,解得x=0.当x变化时,f′(x),f(x)变化情况如下表:
| x | (-∞,0) | 0 | (0,+∞) |
| f′(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及转化思想,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 60° | B. | 30° | C. | 120° | D. | 150° |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{\sqrt{35}}}{18}$ | B. | $\frac{{\sqrt{35}}}{18}$ | C. | $\frac{17}{18}$ | D. | $-\frac{17}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{12}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
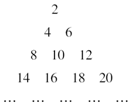 把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).
把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵,记M(r,t)表示该数阵中第r行的第t个数,则数阵中的数2 018对应于(45,19).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
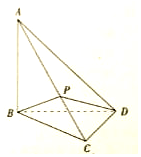 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )| A. | 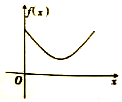 | B. | 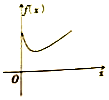 | C. | 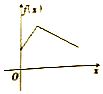 | D. | 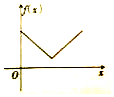 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com