
���� ������������ĵ���������ڵ������IJ���ʽ����������ĵ������伴�ɣ�
������������ĵ��������ݺ����ĵ����Եõ�����a�IJ���ʽ�飬������ɣ�
������������ĵ������õ�����x2-ax+1=0����������ȵ���ʵ����������Ϊm��n�����ݺ����ĵ������жϼ��ɣ�
��� �⣺����$F��x��=f��x��g��x��=\frac{1}{2}a{x^2}lnx��x��0��$��
��${F^'}��x��=axlnx+\frac{1}{2}ax=ax��lnx+\frac{1}{2}��$��
��F�䣨x����0��$x��{e^{-\frac{1}{2}}}$��
��F�䣨x����0����$0��x��{e^{-\frac{1}{2}}}$
��F��x����$��0��{e^{-\frac{1}{2}}}]$�ϵ����ݼ�����$[{e^{-\frac{1}{2}}}��+�ޣ�$�ϵ���������
��$F{��x��_{min}}=F��{e^{-\frac{1}{2}}}��=-\frac{a}{4e}$��F��x������ֵ��
����$G��x��=\frac{1}{2}{x^2}-alnx+��a-1��x$
��${G^'}��x��=x-\frac{a}{x}+a-1=\frac{��x+a����x-1��}{x}$
��$a��0��\frac{1}{e}��x��e$����G��x����$��\frac{1}{e}��1]$�ϵ����ݼ�����[1��e���ϵ���������
Ҫʹ����G��x����$��\frac{1}{e}��e��$����������㣬
��$\left\{\begin{array}{l}G��\frac{1}{e}����0\\ G��1����0\\ G��e����0\end{array}\right.$����$\left\{\begin{array}{l}\frac{1}{{2{e^2}}}+\frac{a-1}{e}+a��0\\ \frac{1}{2}+a-1��0\\ \frac{e^2}{2}+��a-1��e-a��0\end{array}\right.$��
��$\left\{\begin{array}{l}a��\frac{2e-1}{{2{e^2}+2e}}\\ a��\frac{1}{2}\\ a��\frac{{2e-{e^2}}}{2e-2}\end{array}\right.$��
��$\frac{2e-1}{{2{e^2}+2e}}��a��\frac{1}{2}$����a��ȡֵ��Χ��$��\frac{2e-1}{{2{e^2}+2e}}��\frac{1}{2}��$��
������0��a��2����${h^'}��x��=\frac{{-��{x^2}-ax+1��}}{x^2}$�ڣ�0��+�ޣ�������h�䣨x����0��
��h��x���ڣ�0��+�ޣ��ϵ����ݼ�����h��x2��-h��x1����0��
��h��x2��-h��x1�����������ֵ����a��2��
���x2-ax+1=0����������ȵ���ʵ������
����Ϊm��n���Ҳ�����0��m��1��n����$\left\{\begin{array}{l}m+n=a\\ mn=1\end{array}\right.$��
h��x���ڣ�0��m���ϵ����ݼ����ڣ�m��n���ϵ��������ڣ�n��+�ޣ��ϵ����ݼ���
��?x1�ʣ�0��1������h��x1����h��m������?x2�ʣ�1��+�ޣ�����h��x2����h��n����
��[h��x2��-h��x1��]max=h��n��-h��m����
��$M��a��=h��n��-h��m��=��alnn-n+\frac{1}{n}��-��alnm-m+\frac{1}{m}��$=$aln\frac{n}{m}+��m-n��+��\frac{1}{n}-\frac{1}{m}��$��
��$a=m+n=\frac{1}{n}+n$��$m=\frac{1}{n}$������ʽ����ȥa��m��
�ã�$M��a��=��\frac{1}{n}+n��ln{n^2}+2��\frac{1}{n}-n��=2[��\frac{1}{n}+n��lnn+��\frac{1}{n}-n��]$��
��$2��a��e+\frac{1}{e}$����$\frac{1}{n}+n��e+\frac{1}{e}$��n��1��
��$y=x+\frac{1}{x}$��x�ʣ�1��+�ޣ��ϵ�����������n�ʣ�1��e]��
��$�գ�x��=2��\frac{1}{x}+x��lnx+2��\frac{1}{x}-x��$��x�ʣ�1��e]��
${��^'}��x��=2��-\frac{1}{x^2}+1��lnx+2��\frac{1}{x}+x��\frac{1}{x}+2��-\frac{1}{x^2}-1��=2��1-\frac{1}{x^2}��lnx$��x�ʣ�1��e]��
��ա䣨x����0�����գ�x���ڣ�1��e]�ϵ���������
��${[�գ�x��]_{max}}=�գ�e��=2��e+\frac{1}{e}��+2��\frac{1}{e}-e��=\frac{4}{e}$��
��M��a���������ֵΪ$\frac{4}{e}$��
���� ���⿼���˺����ĵ����ԡ���ֵ���⣬���鵼����Ӧ���Լ�ת��˼�룬��һ���ۺ��⣮


 ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �溯������R�ϵ������� | |
| B�� | �溯�����ڣ�-�ޣ�0���ϵ����������ڣ�0��+�ޣ��ϵ������� | |
| C�� | ż�������ڣ�-�ޣ�0���ϵ����ݼ����ڣ�0��+�ޣ��ϵ������� | |
| D�� | ż�������ڣ�-�ޣ�0���ϵ����������ڣ�0��+�ޣ��ϵ����ݼ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
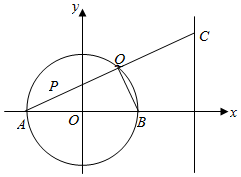 ��֪ԲO��x2+y2=9��ֱ��l1��x=6��ԲO��x���ཻ�ڵ�A��B����ͼ������P��-1��2����ԲO��һ�㣬��QΪԲO����һ�㣨���ڵ�A��B����ֱ��AQ��l1�ཻ�ڵ�C��
��֪ԲO��x2+y2=9��ֱ��l1��x=6��ԲO��x���ཻ�ڵ�A��B����ͼ������P��-1��2����ԲO��һ�㣬��QΪԲO����һ�㣨���ڵ�A��B����ֱ��AQ��l1�ཻ�ڵ�C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3022 | B�� | -3022 | C�� | 2017 | D�� | -2017 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
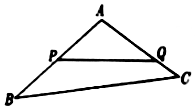 ��ͼ��ij��̬��һ�������ε�ABC��һ��APQ����Ϊˮ������֪��AΪ120�㣬AB��AC�ij��Ⱦ�����200�ף����ڱ߽�AP��AQ����Χǽ����PQ��Χ����ʣ�
��ͼ��ij��̬��һ�������ε�ABC��һ��APQ����Ϊˮ������֪��AΪ120�㣬AB��AC�ij��Ⱦ�����200�ף����ڱ߽�AP��AQ����Χǽ����PQ��Χ����ʣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | ��Ҫ���� | D�� | �Ȳ����Ҳ����Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{2}{7}$ | B�� | $\frac{1}{35}$ | C�� | $\frac{8}{35}$ | D�� | $\frac{7}{24}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com