练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    12．已知数列{an}是等差数列，a1=cot585°，a6=11a1，设Sn为数列{（-1）nan}的前n项和，则S2017=（　　）
    A．3022B．-3022C．2017D．-2017

    分析 利用等差数列的通项公式可得an，计算a2n-a2n+1，利用分组求和即可得出．

    解答 解：a1=cot585°=cot45°=1，
    ∵a6=11a1，∴1+5d=11，解得d=2．
    ∴an=1=2（n-1）=2n-1．
    ∴a2n-a2n+1=4n-1-（4n+1）=-2．
    则S2017=-a1+（a2-a3）+…+（a2016-a2017）=-2017．
    故选：D．

    点评 本题考查了等差数列的通项公式与性质、分组求和，考查了推理能力与计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    2．已知$\vec a=（2，t，t），\vec b=（1-t，2t-1，0）$，则$|\vec b-\vec a|$的最小值是（　　）
    A．$\sqrt{2}$B．$\sqrt{3}$C．$\sqrt{5}$D．$\sqrt{6}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    3．若$α∈（\frac{π}{2}，π）$，且$3cos2α=sin（\frac{π}{4}-α）$，则cos2α的值为（　　）
    A．$-\frac{{\sqrt{35}}}{18}$B．$\frac{{\sqrt{35}}}{18}$C．$\frac{17}{18}$D．$-\frac{17}{18}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

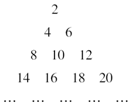    20．把正偶数数列{2n}的各项从小到大依次排成如图的三角形数阵，记M（r，t）表示该数阵中第r行的第t个数，则数阵中的数2 018对应于（45，19）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知f （ x）=$\frac{1}{2}$x2，g （ x）=a ln x（a＞0）．
    （Ⅰ）求函数 F （ x）=f（x）g（x）的极值
    （Ⅱ）若函数 G（ x）=f（x）-g（x）+（a-1）在区间 （$\frac{1}{e}$，e） 内有两个零点，求的取值范围；
    （Ⅲ）函数 h（ x）=g （ x ）-x+$\frac{1}{x}$，设 x1∈（0，1），x2∈（1，+∞），若 h（ x 2）-h（ x 1）存在最大值，记为 M （a），则当 a≤e+1$\frac{1}{e}$时，M （a） 是否存在最大值？若存在，求出其最大值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．已知圆x2+y2=1和圆外一点P（1，2），过点P作圆的切线，则切线方程为x=1或3x-4y+5=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

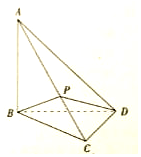    4．《九章算术》中，将四个面都为直角三角形的四面体称之为鳖臑，如图，在鳖臑A-BCD中，AB⊥平面BCD，且BD⊥CD，AB=BD=CD，点P在棱AC上运行，设CP的长度为x，若△PBD的面积为f（x），则f（x）的图象大致是（　　）
    A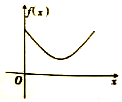．B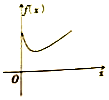．C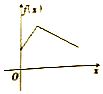．D．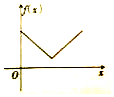

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．某篮球运动员在最近5场比赛中所得分数分别为12，a，8，15，23，其中a＞0，若该运动员在这5场比赛中得分的中位数为12，则得分的平均数不可能为（　　）
    A．$\frac{68}{5}$B．$\frac{69}{5}$C．$\frac{71}{5}$D．14

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知F是抛物线C：y=2x2的焦点，点P（x，y）在抛物线C上，且x=1，则|PF|=（　　）
    A．$\frac{9}{8}$B．$\frac{3}{2}$C．$\frac{17}{8}$D．$\frac{5}{2}$

    查看答案和解析>>

    同步练习册答案