
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
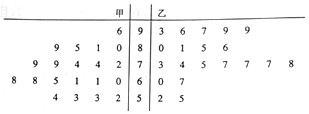
分析 (1)根据茎叶图计算甲、乙两班化学成绩前10名学生的平均分即可;
(2)确定基本事件的个数,即可求出这2人来自不同班级的概率;
(3)填写列联表,计算K2,对照数表即可得出结论.
解答 解:(1)甲班样本化学成绩前十的平均分为$\overline{x_甲}=\frac{1}{10}(72+74+74+79+79+80+81+85+89+96)=80.9$;
乙班样本化学成绩前十的平均分为$\overline{x_乙}=\frac{1}{10}(78+80+81+85+86+93+96+97+99+99)=89.4$;
甲班样本化学成绩前十的平均分远低于乙班样本化学成绩前十的平均分,大致可以判断“高效课堂”教学方式的教学效果更佳.
(2)样本中成绩6(0分)以下的学生中甲班有4人,记为:a,b,c,d,乙班有2人,记为:1,2.
则从a,b,c,d,1,2六个元素中任意选2个的所有基本事件如下:ab,ac,ad,a1,a2,bc,bd,b1,b2,cd,c1,c2,d1,d2,12,一共有15个基本事件,
设A表示“这2人来自不同班级”有如下:a1,a2,b1,b2,c1,c2,d1,d2,一共有8个基本事件,
所以$P(A)=\frac{8}{15}$.
(3)
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
点评 本题考查了计算平均数与独立性检验的应用问题,考查概率的计算,解题时应根据列联表求出观测值,对照临界值表得出结论,是基础题目.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中数学 来源: 题型:选择题
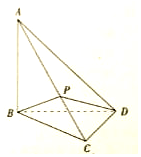 《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )
《九章算术》中,将四个面都为直角三角形的四面体称之为鳖臑,如图,在鳖臑A-BCD中,AB⊥平面BCD,且BD⊥CD,AB=BD=CD,点P在棱AC上运行,设CP的长度为x,若△PBD的面积为f(x),则f(x)的图象大致是( )| A. | 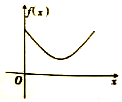 | B. | 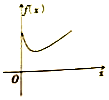 | C. | 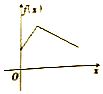 | D. | 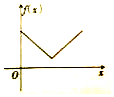 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{8}$ | B. | $\frac{3}{2}$ | C. | $\frac{17}{8}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
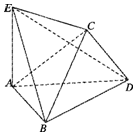 将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.
将边长为2的正方形ABCD沿对角线BD折叠,使得平面ABD⊥平面CBD,AE⊥平面ABD,且AE=$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| a1 | a2 | … | an |
| b1 | b2 | … | bn |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com