
分析 (1)令F(x)=0,求出函数的零点即可;
(2)关于p:求出函数的导数,$a-\frac{1}{x}≤0$在$[{\frac{1}{4},\frac{1}{2}}]$恒成立,求出a的范围,关于q:根据二次函数的性质求出a的范围,取交集即可.
解答 解(1)∵a=0,∴F(x)=ln(x2-2x)-lnx,
由F(x)=0得x2-2x=x,∴x=0或x=3,
又因为F(x)的定义域{x|x>2},
∴x=0舍去,
∴F(x)的零点为3;
(2)∵${f^'}(x)=a-\frac{1}{x},且f(x)在[{\frac{1}{4},\frac{1}{2}}]$递减,
∴$a-\frac{1}{x}≤0$在$[{\frac{1}{4},\frac{1}{2}}]$恒成立,
∴a≤2,
又因为g(x)的定义域为R,
所以x2-2x+a>0对一切实数恒成立,
∴4-4a<0,∴a>1,
∵p∧q为真,
∴1<a≤2.
点评 本题考查了函数的零点问题,考查函数恒成立问题以及二次函数的性质,是一道中档题.


科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
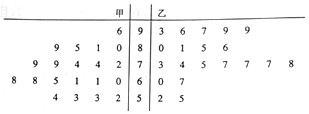
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| Y X | 有震 | 无震 | 合计 |
| 水位有变化 | 100 | 900 | 1 000 |
| 水位无变化 | 80 | 620 | 7 00 |
| 合计 | 180 | 1520 | 1700 |
| P(X2≥x0) | 0.15 | 0.1 | 0.05 |
| x0 | 2.072 | 2.706 | 3.841 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com