
| a1 | a2 | … | an |
| b1 | b2 | … | bn |
分析 (Ⅰ)根据新定义计算即可,
(Ⅱ)ai=i(i=1,2,…,n),则无论b1,b2,…,bn填写的顺序如何,都有${S_n}={n^2}$,根据新定义求出即可,
(Ⅲ)方法一:交换每一列中两个数的位置,所得的Sn的值不变,不妨设ai>bi,记$A=\sum_{i=1}^n{a_i}$,$B=\sum_{i=1}^n{b_i}$,求出Sn=A-B,即可证明,
方法二:考虑如下表所示的任意两种不同的填法,①若在两种填法中k都位于同一行,②若在两种填法中k位于不同行,即可证明
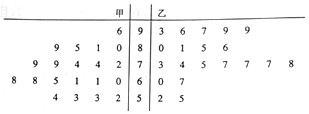
解答 解:(Ⅰ)∵a1=1,a2=3,a3=5,
∴b1,b2,b3值为2,4,6
∴S3=|a1-b1|+|a2-b2|+|a3-b3|=|1-b1|+|3-b2|+|5-b3|,
∴S3的所有可能的取值为3,5,7,9.
(Ⅱ) 令ai=i(i=1,2,…,n),则无论b1,b2,…,bn填写的顺序如何,都有${S_n}={n^2}$.
因为 ai=i,
所以 bi∈{n+1,n+2,…,2n},(i=1,2,…,n).
因为 ai<bi(i=1,2,…,n),
所以 ${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\sum_{i=1}^n{({b_i}-{a_i})}=\sum_{i=1}^n{b_i}-\sum_{i=1}^n{a_i}=\sum_{i=n+1}^{2n}i-\sum_{i=1}^ni={n^2}$.
注:{a1,a2,…,an}={1,2,…,n},或{a1,a2,…,an}={n+1,n+2,…,2n}均满足条件.
(Ⅲ)解法一:显然,交换每一列中两个数的位置,所得的Sn的值不变.
不妨设ai>bi,记$A=\sum_{i=1}^n{a_i}$,$B=\sum_{i=1}^n{b_i}$,其中i=1,2,…,n.
则 ${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\sum_{i=1}^n{({a_i}-{b_i})}=\sum_{i=1}^n{a_i}-\sum_{i=1}^n{b_i}=A-B$.
因为 $A+B=\sum_{i=1}^{2n}i=\frac{2n(2n+1)}{2}=n(2n+1)$,
所以 A+B与n具有相同的奇偶性.
又因为 A+B与A-B具有相同的奇偶性,
所以 Sn=A-B与n的奇偶性相同,
所以 Sn的所有可能取值的奇偶性相同.
解法二:显然,交换每一列中两个数的位置,所得的Sn的值不变.
考虑如下表所示的任意两种不同的填法,${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}$,${S'_n}=\sum_{i=1}^n{|{{a'}_i}-{{b'}_i}|}$,不妨设ai<bi,a'i<b'i,其中 i=1,2,…,n.
| a1 | a2 | … | an | ${a_1}^′$ | ${a_2}^′$ | … | ${a_n}^′$ | |
| b1 | b2 | … | bn | ${b_1}^′$ | ${b_2}^′$ | … | ${b_n}^′$ |
点评 本题考查了新定义的应用,以及数列求和问题,考查了学生的分析问题和解决问题的能力,属于难题.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:高中数学 来源: 题型:选择题
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
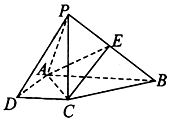 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com