练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．下列函数中，既是偶函数又在区间（0，+∞）上单调递增的是（　　）
    A．$y=\frac{1}{x^2}$B．y=${（\frac{1}{2}）}^{|x|}$C．y=lg xD．y=|x|-1

    分析 分别函数的奇偶性、单调性，即可得出结论．

    解答 解：A中函数$y=\frac{1}{x^2}$是偶函数且在（0，+∞）上单调递减，故A错误；
    B中函数是偶函数且在（0，+∞）上单调递减，故B错误；
    C中函数不是偶函数，故C错误；
    D中函数是偶函数且在（0，+∞）上单调递增，
    故选D．

    点评 本题考查函数的奇偶性、单调性，考查学生的计算能力，属于中档题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    17．已知圆x2+y2=1和圆外一点P（1，2），过点P作圆的切线，则切线方程为x=1或3x-4y+5=0．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．设正三棱锥A-BCD内接于球O，BC=1，E为AB的中点，AC⊥DE，则球的半径为（　　）
    A．$\frac{{\sqrt{3}}}{3}$B．$\frac{{\sqrt{2}}}{2}$C．$\frac{{\sqrt{6}}}{4}$D．$\frac{{\sqrt{10}}}{4}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知函数$f（x）=\frac{1}{x+1}$，点O为坐标原点，点${A_n}（{n，f（n）}）（{n∈{N^*}}）$，向量$\vec i=（{0，1}）$，θn是向量$\overrightarrow{O{A}_{n}}$与$\vec i$的夹角，则$\frac{{cos{θ_1}}}{{sin{θ_1}}}+\frac{{cos{θ_2}}}{{sin{θ_2}}}+…+\frac{{cos{θ_{2017}}}}{{sin{θ_{2017}}}}$的值为$\frac{2017}{2018}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知F是抛物线C：y=2x2的焦点，点P（x，y）在抛物线C上，且x=1，则|PF|=（　　）
    A．$\frac{9}{8}$B．$\frac{3}{2}$C．$\frac{17}{8}$D．$\frac{5}{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．若实数x，y满足：$\left\{{\begin{array}{l}{y≥2x-2}\\{y≥-x+1}\\{y≤x+1}\end{array}}\right.$，则z=3x-y的最大值是（　　）
    A．3B．4C．5D．6

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．如表，将数字1，2，3，…，2n（n≥3）全部填入一个2行n列的表格中，每格填一个数字．第一行填入的数字依次为a1，a2，…，an，第二行填入的数字依次为b1，b2，…，bn．
    记${S_n}=\sum_{i=1}^n{|{a_i}-{b_i}|}=\;|{a_1}-{b_1}|+|{a_2}-{b_2}|+…+|{a_n}-{b_n}|$．
    a1a2…an
    b1b2…bn
    （Ⅰ）当n=3时，若a1=1，a2=3，a3=5，写出S3的所有可能的取值；
    （Ⅱ）给定正整数n．试给出a1，a2，…，an的一组取值，使得无论b1，b2，…，bn填写的顺序如何，Sn都只有一个取值，并求出此时Sn的值；
    （Ⅲ）求证：对于给定的n以及满足条件的所有填法，Sn的所有取值的奇偶性相同．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．某商场为吸引顾客消费推出一项优惠活动．活动规则如下：消费额每满100元可转动如图所示的转盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置．若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券．例如：消费218元，可转动转盘2次，所获得的返券金额是两次金额之和．
    （Ⅰ）若某位顾客消费128元，求返券金额不低于30元的概率；
    （Ⅱ）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记为X（元）．求X=60时的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

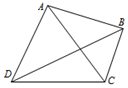    11．蓝军和红军进行军事演练，蓝军在距离$\sqrt{3}$的军事基地C和D，测得红军的两支精锐部队分别在A处和B处，且∠ADB=30°，∠BDC=30°，∠DCA=60°，∠ACB=45°，如图所示，则红军这两支精锐部队间的距离是（　　）
    A．$\frac{{\sqrt{6}}}{2}$B．$\sqrt{6}$C．$\frac{3}{4}$D．$\sqrt{3}$

    查看答案和解析>>

    同步练习册答案