
| A. | $\frac{{\sqrt{3}}}{3}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{6}}}{4}$ | D. | $\frac{{\sqrt{10}}}{4}$ |
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,e2) | C. | (e,+∞) | D. | (1,e) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
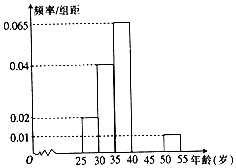 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | -4 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $y=\frac{1}{x^2}$ | B. | y=${(\frac{1}{2})}^{|x|}$ | C. | y=lg x | D. | y=|x|-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com