
分析 kAB=$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$,kAC=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$.由A,B,C三点共线,可得kAB=kAC.化简整理即可得出.
解答 证明:kAB=$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$,kAC=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$.
∵A,B,C三点共线,∴kAB=kAC.
∴$\frac{{x}_{2}^{3}-{x}_{1}^{3}}{{x}_{2}-{x}_{1}}$=$\frac{{x}_{3}^{3}-{x}_{1}^{3}}{{x}_{3}-{x}_{1}}$.
∴${x}_{2}^{2}$+x1x2+${x}_{1}^{2}$=${x}_{3}^{2}$+x1x3+${x}_{1}^{2}$,
∴(x2-x3)(x1+x2+x3)=0,∵x2≠x3.
∴x1+x2+x3=0.
点评 本题考查了直线共线与斜率的关系、乘法公式,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{7}$ | B. | $\frac{1}{35}$ | C. | $\frac{8}{35}$ | D. | $\frac{7}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
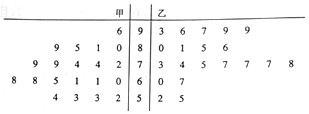
| 甲班 | 乙班 | 总计 | |
| 成绩优良 | 10 | 16 | 26 |
| 成绩不优良 | 10 | 4 | 14 |
| 总计 | 20 | 20 | 40 |
| P(K2≥k0) | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{2}+i$ | B. | $\sqrt{2}-i$ | C. | $1+\sqrt{2}i$ | D. | $1-\sqrt{2}i$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $\sqrt{5}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | a>c>b |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com