
| A. | min{|a+b|,|a-b|}≤min{|a|,|b|} | B. | max{|a+b|,|a-b|}≤max{|a|,|b|} | ||
| C. | min{|a+b|2,|a-b|2}≥|a|2+|b|2 | D. | max{|a+b|2,|a-b|2}≥{|a|2+|b|2 |
分析 通过转化为向量加法与减法的几何意义,结合题目中的取最大与最小值,对选项中的问题进行分析判断,对错误选项进行排除即可.
解答 解:∵a=x1+y1i,b=x2+y2i,x1,y1,x2,y2∈R,
∴可记$\overrightarrow{a}$=(x1,y1),$\overrightarrow{b}$=(x2,y2),则|$\overrightarrow{a}$|=|a|,|$\overrightarrow{b}$|=|b|,
∴|$\overrightarrow{a}$±$\overrightarrow{b}$|2=|$\overrightarrow{a}$|2+|$\overrightarrow{b}$|2±2|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,
∴max{|a+b|2,|a-b|2}≥|a|2+|b|2成立,D正确;
对于A,当$\overrightarrow{a}$⊥$\overrightarrow{b}$时,易知不等式不成立,C不正确;
对于B,当$\overrightarrow{a}$=$\overrightarrow{b}$且均不为零向量时,易知不等式不成立,B不正确;
对于C,当$\overrightarrow{a}$=$\overrightarrow{b}$且均不为零向量时,易知不等式不成立,C不正确;
故选:D.
点评 本题考查复数的几何意义的应用问题,解题时应排除法,对错误选项进行举反例说明,注意解题方法的积累,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
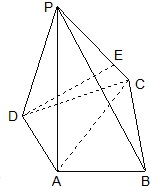 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AC⊥AB,AD⊥DC,∠DAC=60°,PA=AC=2,AB=1,点E在棱PC上,且DE⊥PB.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com