
分析 (1)直接由题意求出椭圆和双曲线的半焦距c,结合隐含条件求得椭圆的短半轴长,则椭圆方程可求;联立椭圆方程和抛物线方程,求得P的坐标,代入双曲线方程,再与双曲线的隐含条件联立求得m,n,则双曲线方程可求;
(2)设出Q的坐标,由已知列式求得Q的坐标,再由勾股定理求出Q到双曲线左焦点的距离,利用双曲线定义求得实半轴长,则双曲线的离心率可求.
解答 解:(1)由抛物线y2=4x,得抛物线的交点F(1,0),
∴椭圆的半焦距c=1,则b2=a2-c2=4-1=3,
∴椭圆方程为$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$,
联立$\left\{\begin{array}{l}{{y}^{2}=4x}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,解得:P($\frac{2}{3},\frac{2\sqrt{6}}{3}$),
则$\left\{\begin{array}{l}{\frac{4}{9{m}^{2}}-\frac{8}{3{n}^{2}}=1}\\{{m}^{2}+{n}^{2}=1}\end{array}\right.$,解得:${m}^{2}=\frac{1}{9},{n}^{2}=\frac{8}{9}$.
∴双曲线方程为$\frac{{x}^{2}}{\frac{1}{9}}-\frac{{y}^{2}}{\frac{8}{9}}=1$;
(2)设Q(${x}_{0},2\sqrt{{x}_{0}}$),则$({x}_{0}+1)^{2}=(\sqrt{3})^{2}+{{x}_{0}}^{2}$,解得x0=1,
则QF与x轴垂直,设双曲线的左焦点为F′,
则(QF′)2=QF2+(2c)2=22+22=8,∴$QF′=2\sqrt{2}$,
则$2m=QF′-QF=2\sqrt{2}-2$,m=$\sqrt{2}-1$.
则双曲线的离心率e=$\frac{1}{\sqrt{2}-1}=\sqrt{2}+1$.
点评 本题考查椭圆方程与双曲线方程的求法,考查了圆与抛物线相交问题,关键是对抛物线定义的灵活运用,是中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
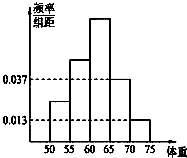 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | min{|a+b|,|a-b|}≤min{|a|,|b|} | B. | max{|a+b|,|a-b|}≤max{|a|,|b|} | ||
| C. | min{|a+b|2,|a-b|2}≥|a|2+|b|2 | D. | max{|a+b|2,|a-b|2}≥{|a|2+|b|2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com