
分析 由已知中sinα=-$\frac{3}{5}$,α∈(-$\frac{π}{2}$,0),求出cosα值,代入两角和的余弦公式,可得答案.
解答 解:∵sinα=-$\frac{3}{5}$,α∈(-$\frac{π}{2}$,0),
∴cosα=$\sqrt{1-{sin}^{2}α}$=$\frac{4}{5}$,
∴cos(α+$\frac{5π}{4}$)=cosαcos$\frac{5π}{4}$-sinαsin$\frac{5π}{4}$=$-\frac{7\sqrt{2}}{10}$,
故答案为:$-\frac{7\sqrt{2}}{10}$.
点评 本题考查的知识点是两角和与差的余弦公式,难度不大,属于基础题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
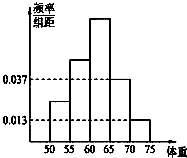 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | min{|a+b|,|a-b|}≤min{|a|,|b|} | B. | max{|a+b|,|a-b|}≤max{|a|,|b|} | ||
| C. | min{|a+b|2,|a-b|2}≥|a|2+|b|2 | D. | max{|a+b|2,|a-b|2}≥{|a|2+|b|2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com