
| A�� | 0 | B�� | 1 | C�� | 2 | D�� | 3 |
���� ������$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$ȡ������˵�����۴���
������$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$���ٸ���k���������ۼ��ɵó���$\frac{n+1}{n}$һ����������˵����һ���������
����$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$$��\frac{n+1}{2n}$��1���ó����۳���
�ܵ�$\frac{k}{1-k}$Ϊ������ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$=1���ó�������ȷ��
��� �⣺�ٵ�k=$\frac{1}{2}$ʱ��${a}_{n}=n��\frac{1}{2}��^{n}$����$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1����\frac{1}{2}��^{n+1}}{n��\frac{1}{2}��^{n}}$=$\frac{n+1}{2n}$����n=1ʱ��a1=a2���������{an}���ǵݼ����У��ʢٲ���ȷ��
�ڵ�$\frac{1}{2}$��k��1ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$=k+$\frac{k}{n}$����n��$\frac{1-k}{k}$ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$��1����������{an}һ���������ڲ���ȷ��
�۵�0��k��$\frac{1}{2}$ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$$��\frac{n+1}{2n}$��1����an+1��an��
�������{an}Ϊ�ݼ����У�����ȷ��
�ܵ�$\frac{k}{1-k}$Ϊ������ʱ��$\frac{{a}_{n+1}}{{a}_{n}}$=$\frac{��n+1��{k}^{n+1}}{n{k}^{n}}$=$\frac{��n+1��k}{n}$=1���������{an}����������ȵ������ʢ���ȷ��
��ѡ��C
���� ���⿼�������еĵ����ԡ��������۵�˼�뷽�������������������ͼ����������������⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ������x��2������x2��4 | B�� | ��x��2������x2��4 | ||
| C�� | ����x��2��ʹx2��4 | D�� | ����x��2��ʹx2��4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{2015}$ | B�� | -$\frac{1}{2015}$ | C�� | $\frac{1}{4030}$ | D�� | -$\frac{1}{4030}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
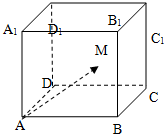 ��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�ڣ�����������棩��ȡһ��M����$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$��1�ĸ����ǣ�������
��ͼ�����ⳤΪ2��������ABCD-A1B1C1D1�ڣ�����������棩��ȡһ��M����$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$��1�ĸ����ǣ�������| A�� | $\frac{5}{6}$ | B�� | $\frac{1}{2}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com