
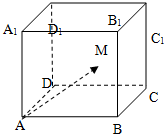
 如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )
如图,在棱长为2的正方体ABCD-A1B1C1D1内(含正方体表面)任取一点M,则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率是( )| A. | $\frac{5}{6}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
分析 本题是几何概型问题,欲求点M满足则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率,先以A为原点建立空间直角坐标系,由数量积公式得出点M到平面ABCD的距离大于等于$\frac{1}{2}$,点M的轨迹是正方体的$\frac{3}{4}$,求出其体积,再根据几何概型概率公式结合正方体的体积的方法求解即可
解答 解:本题是几何概型问题,正方体的体积为V=8,
以A为原点建立空间直角坐标系,AB为x轴,AD为y轴,AA1为z轴.
那么A(0,0,0),A1(0,0,2)
设M(x,y,z),那么x,y,z∈[0,2]
∴$\overrightarrow{AM}$=(x,y,z),$\overrightarrow{A{A}_{1}}$=(0,0,2)
则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1,即2z≥1,z≥$\frac{1}{2}$.
即点M与平面ABCD的距离大于等于$\frac{1}{2}$,点M的轨迹是正方体的$\frac{3}{4}$,其体积为:V1=$\frac{3}{4}$,
则$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$≥1的概率p为$\frac{3}{4}$;
故选:D.
点评 本小题主要考查几何概型、几何概型的应用、几何体的体积等基础知识,考查空间想象能力、化归与转化思想.属于中档题.


科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>1 | B. | a>-1 | C. | a≤1 | D. | a≤-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,9) | B. | (-9,1) | C. | (-∞,-1)∪(9,+∞) | D. | (-∞,-9)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
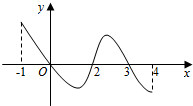 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com