
| ΡξΖί | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| ¥ζΚ≈t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| œζ έΕνy | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
Ζ÷Έω Θ®1Θ©”–ΗχΕ®ΒΡΉχ±ξœΒ÷–Οη≥ωΗςΉι ΐΨίΕ‘”ΠΒΡΒψΘ§Ω…ΒΟΡξΖί¥ζΚ≈”κœζ έΕνΒΡ…ΔΒψΆΦΘΜ
Θ®2Θ©ΗυΨίΥυΗχΒΡ ΐΨίΘ§άϊ”ΟΉν–ΓΕΰ≥ΥΖ®Ω…ΒΟΚα±ξΚΆΉί±ξΒΡΤΫΨυ ΐΘ§Κα±ξΚΆΉί±ξΒΡΜΐΒΡΚΆΘ§”κΚα±ξΒΡΤΫΖΫΚΆΘ§¥ζ»κΙΪ Ϋ«σ≥ωbΒΡ÷ΒΘ§‘Ό«σ≥ωaΒΡ÷ΒΘ§–¥≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΘ°
Θ®3Θ©ΗυΨί…œ“ΜΈ Ήω≥ωΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘ§¥ζ»κΥυΗχΒΡtΒΡ÷ΒΘ§‘Λ≤βΗΟΒΊ«χ2015ΡξΒΡœζ έΕνΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©ΡξΖί¥ζΚ≈”κœζ έΕνΒΡ…ΔΒψΆΦ»γœ¬Υυ ΨΘΚ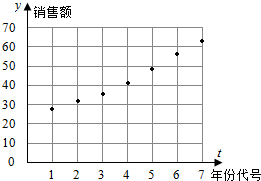
Θ®2Θ©”…“―÷Σ÷–ΒΡ ΐΨίΩ…ΒΟΘΚ
$\overline{t}$=$\frac{1}{7}$Θ®1+2+3+4+5+6+7Θ©=4Θ§
$\overline{y}$=$\frac{1}{7}$Θ®27+31+35+41+49+56+62Θ©=43Θ§
$\sum _{i=1}^{7}{t}_{i}{y}_{i}$=1373Θ§$\sum _{i=1}^{7}{{t}_{i}}^{2}$=140Θ§
Ι $\hat{b}$=$\frac{\sum _{i=1}^{7}{t}_{i}{y}_{i}-7\overline{t}\overline{y}}{\sum _{i=1}^{7}{{t}_{i}}^{2}-7{\overline{t}}^{2}}$=$\frac{1373-1204}{140-112}$=$\frac{169}{28}$Γ÷6.04Θ§
‘ρ$\hat{a}$=$\overline{y}$-6.04$\overline{t}$=18.84Θ§
Ι yΙΊ”ΎtΒΡœΏ–‘ΜΊΙιΖΫ≥Χ$\hat{y}$=6.04x+18.84Θ§
Θ®3Θ©2015ΡξΒΡΡξΖί¥ζΚ≈ΈΣ8Θ§
Β±t=8 ±Θ§$\hat{y}$=6.04ΓΝ8+18.84=67.16Θ§
Ι ‘Λ≤βΗΟΤσ“Β2015ΡξΒΡœζ έΕν‘ΦΈΣ67.16“Ύ‘Σ
ΒψΤά ±ΨΧβΩΦ≤ιœΏ–‘ΜΊΙιΖ÷ΈωΒΡ”Π”ΟΘ§±ΨΧβΫβΧβΒΡΙΊΦϋ «άϊ”ΟΉν–ΓΕΰ≥ΥΖ®»œ’φΉω≥ωœΏ–‘ΜΊΙιΖΫ≥ΧΒΡœΒ ΐΘ§’β «’ϊΗωΧβΡΩΉωΕ‘ΒΡ±Ί±ΗΧθΦΰΘ§±ΨΧβ «“ΜΗωΜυ¥ΓΧβΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $\frac{1}{3}$ | BΘ° | $\frac{1}{5}$ | CΘ° | $\frac{1}{7}$ | DΘ° | $\frac{1}{9}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | $Θ®{1Θ§1+\frac{{\sqrt{2}}}{2}}Θ©$ | BΘ° | $Θ®{1+\frac{{\sqrt{2}}}{2}Θ§+Γό}Θ©$ | CΘ° | $Θ®{1Θ§1+\sqrt{2}}Θ©$ | DΘ° | $Θ®{1+\sqrt{2}Θ§+Γό}Θ©$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | Ε‘»Έ“βxΓί2Θ§ΕΦ”–x2ΘΦ4 | BΘ° | Ε‘xΘΦ2Θ§ΕΦ”–x2Γί4 | ||
| CΘ° | ¥φ‘ΎxΓί2Θ§ Ιx2ΘΦ4 | DΘ° | ¥φ‘ΎxΘΦ2Θ§ Ιx2Γί4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 1 | BΘ° | 2 | CΘ° | 3 | DΘ° | 4 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | {Θ®1Θ§1Θ©} | BΘ° | {Θ®-1Θ§1Θ©Θ§Θ®1Θ§1Θ©} | CΘ° | $[{\frac{1}{2}Θ§+Γό}Θ©$ | DΘ° | $[{\frac{{\sqrt{2}}}{2}Θ§+Γό}Θ©$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚΗΏ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
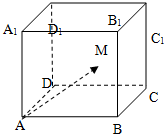 »γΆΦΘ§‘Ύάβ≥ΛΈΣ2ΒΡ’ΐΖΫΧεABCD-A1B1C1D1ΡΎΘ®Κ§’ΐΖΫΧε±μΟφΘ©»Έ»Γ“ΜΒψMΘ§‘ρ$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$Γί1ΒΡΗ≈¬ «Θ®ΓΓΓΓΘ©
»γΆΦΘ§‘Ύάβ≥ΛΈΣ2ΒΡ’ΐΖΫΧεABCD-A1B1C1D1ΡΎΘ®Κ§’ΐΖΫΧε±μΟφΘ©»Έ»Γ“ΜΒψMΘ§‘ρ$\overrightarrow{A{A}_{1}}$•$\overrightarrow{AM}$Γί1ΒΡΗ≈¬ «Θ®ΓΓΓΓΘ©| AΘ° | $\frac{5}{6}$ | BΘ° | $\frac{1}{2}$ | CΘ° | $\frac{2}{3}$ | DΘ° | $\frac{3}{4}$ |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com