
分析 利用|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(2\overrightarrow{a}-\overrightarrow{b})^{2}}$计算即可.
解答 解:∵向量$\overrightarrow{a}$与$\overrightarrow{b}$的方向相反,
∴cos<$\overrightarrow a$,$\overrightarrow b$>=cosπ=-1,
又∵|$\overrightarrow{a}$|=3、|$\overrightarrow{b}$|=4,
∴$\overrightarrow{a}$•$\overrightarrow{b}$=|$\overrightarrow{a}$|•|$\overrightarrow{b}$|cos<$\overrightarrow a$,$\overrightarrow b$>=-12,
∴$(2\overrightarrow{a}-\overrightarrow{b})^{2}$=4${\overrightarrow{a}}^{2}$-4$\overrightarrow{a}$•$\overrightarrow{b}$+${\overrightarrow{b}}^{2}$=36+48+16=100,
∴|2$\overrightarrow{a}$-$\overrightarrow{b}$|=$\sqrt{(2\overrightarrow{a}-\overrightarrow{b})^{2}}$=10.
点评 本题考查平面向量数量积的性质及其计算,注意解题方法的积累,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 |
| 代号t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 销售额y | 27 | 31 | 35 | 41 | 49 | 56 | 62 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
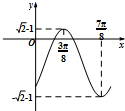 已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.
已知函数f(x)=asin(ωx+θ)-b的部分图象如图,其中ω>0,|θ|<$\frac{π}{2}$,a,b分别是△ABC的角A,B所对的边,$cosC=f(\frac{C}{2})+1$,则△ABC的面积S=$\frac{{\sqrt{10}}}{5}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com