
分析 如果f(x)≤g(x)在[-2,+∞)上恒成立,则对x的取值进行分类讨论,利用孤立参数法,结合导数法,可各各种情况下k的取值范围,最后综合讨论结果,可得答案.
解答 解:若f(x)≤g(x)恒成立,
则-2x3+3x2+12x-11≤kx+9恒成立,
当x=0时,-11≤9恒成立,k∈R;
当-2≤x<0时,有k≤-2x2+3x+12-$\frac{20}{x}$,
设h(x)=-2x2+3x+12-$\frac{20}{x}$=-2$(x-\frac{3}{4})^{2}$+$\frac{105}{8}$-$\frac{20}{x}$,
当-2≤x<0时,y=-2$(x-\frac{3}{4})^{2}$+$\frac{105}{8}$为增函数,y=-$\frac{20}{x}$也为增函数,
故h(x)为增函数,
∴h(x)≥h(-2)=8,
即k≤8
当x>0时,令f′(x)=-6x2+6x+12=0,解得x=-1,x=2,
当x∈(0,2)时,f′(x)>0,函数f(x)为增函数,
当x∈(2,+∞)时,f′(x)<0,函数f(x)为减函数,
故当x=2时,函数取最大值9,∈∞
若f(x)≤g(x)恒成立,
则k≥0,
综上所述,0≤k≤8,
即满足f(x)≤g(x)恒成立的k的取值范围为[0,8]
点评 本题考查的知识点是函数的最值及其几何意义,函数恒成立问题,难度较大,分类比较复杂,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x}{2}$-3<$\frac{x}{3}$-3 | B. | $\left\{\begin{array}{l}{x-2<0}\\{2-3x>1}\end{array}\right.$ | C. | x2-2x>0 | D. | |x-1|<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
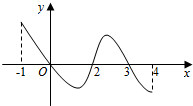 已知函数f(x)的定义域为[-1,4],部分对应值如表,
已知函数f(x)的定义域为[-1,4],部分对应值如表,| x | -1 | 0 | 2 | 3 | 4 |
| f(x) | 1 | 2 | 0 | 2 | 0 |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
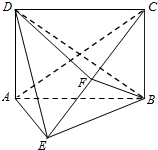 如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,
如图,在四棱锥E-ABCD中,底面ABCD为矩形,平面ABCD⊥平面ABE,∠AEB=90°,BE=BC,F为CE的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com