
分析 (I)设Q(4,y0),代入x2=2py,结合|QF|=$\frac{5}{4}$|PQ|.求出p,即可求解C的方程.
(II)求出A(-4,4),假设存在满足条件的直线l,设M(x1,y1),N(x2,y2),联立方程组利用韦达定理以及判别式,通过三角形是直角三角形,数量积为0求解k即可.
解答 解:(I)设Q(4,y0),代入x2=2py,
得${y_0}=\frac{8}{p}\;,\;∴|{PQ}|=\frac{8}{p}\;,\;|{QF}|=\frac{p}{2}+{y_0}=\frac{p}{2}+\frac{8}{p}$.
由题设得$\frac{p}{2}+\frac{8}{p}=\frac{5}{4}×\frac{8}{p}$,解得p=-2(舍去)或p=2,
∴C的方程为x2=4y…(4分)
(II)由x2=4y知,点A(-4,4),假设存在满足条件的直线l,
设M(x1,y1),N(x2,y2),联立方程组$\left\{\begin{array}{l}{x^2}=4y\\ y=kx+4\end{array}\right.$得x2-4kx-16=0,
△=16(k2+4)>0,
x1+x2=4k,x1x2=-16…(6分)
由题意得$\overrightarrow{AM}•\overrightarrow{AN}=({x_1}+4,{y_1}-4)({x_2}+4,{y_2}-4)=({x_1}+4)({x_2}+4)+{k^2}{x_1}{x_2}$=(1+k2)x1x2+4(x1+x2)+16=0,…(10分)
代入x1+x2=4k,x1x2=-16得-(1+k2)+k+1=0,
解得k=0(舍)或k=1…(12分)
点评 本题考查抛物线方程的求法,直线与抛物线的位置关系的综合应用,考查分析问题解决问题的能力,转化思想的应用.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
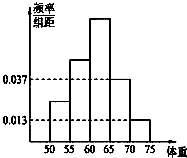 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com