
 如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:
如图1,在边长为12的正方形AA′A${\;}_{1}^{′}$A1中,BB1∥CC1∥AA1,且AB=3,且BC=4,AA${\;}_{1}^{′}$分别交BB1,CC1于点P,Q,将该正方形沿BB1,CC1折叠,使得A′A${\;}_{1}^{′}$与AA1重合,构成图2所示的三棱柱ABC-A1B1C1,在图2中:分析 (1)由BB1⊥平面ABC得BB1⊥AB;由勾股定理得AB⊥BC,从而证得AB⊥平面BCC1B1,从而AB⊥PQ.
(2)建系,求得平面APQ的一个法向量为设$\overrightarrow{AM}$=λ$\overrightarrow{AC}$,根据题意$\overrightarrow{BM}$-$\overrightarrow{n}$=0求得λ,进而求得点M到平面PAQ的距离.
解答 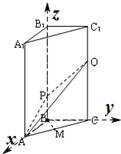 (1)∵BB1⊥平面ABC,
(1)∵BB1⊥平面ABC,
∴BB1⊥AB;
由勾股定理得AB⊥BC,
∵BC?平面BCC1B1,BB1?平面BCC1B1,BB1∩BC=B
∴AB⊥平面BCC1B1,
∵PQ?平面BCC1B1,
∴AB⊥PQ
(2)如图建系,由条件得BP=3,CQ=7,可求得平面APQ的
一个法向量为N=(1,-1,1).设$\overrightarrow{AM}$=λ$\overrightarrow{AC}$,则$\overrightarrow{BM}$=$\overrightarrow{BA}$+$\overrightarrow{AM}$=(3-3λ,4λ,0),
由题意有$\overrightarrow{BM}$-$\overrightarrow{n}$=0,
解得λ=$\frac{3}{7}$,则d=$\frac{|\overrightarrow{AM}-\overrightarrow{n}|}{|\overrightarrow{n}|}$=$\sqrt{3}$.
点评 本题主要考查了线面垂直的判定定理的运用,法向量的运用.考查了学生综合分析问题解决问题的能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
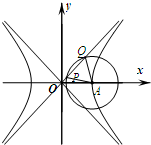 如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,则双曲线C的离心率为( )
如图,已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右顶点为A,O为坐标原点,以A为圆心的圆与双曲线C的某渐近线交于两点P,Q.若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$,则双曲线C的离心率为( )| A. | $\sqrt{3}$ | B. | $\frac{2\sqrt{13}}{5}$ | C. | $\frac{\sqrt{7}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 对任意x≥2,都有x2<4 | B. | 对x<2,都有x2≥4 | ||
| C. | 存在x≥2,使x2<4 | D. | 存在x<2,使x2≥4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 学校抽取每个班级座号为21-30号的同学检查作业完成情况,这是分层抽样 | |
| B. | 可以通过频率分布直方图中最高小矩形的高来估计这组数据的众数 | |
| C. | 设随机变量ξ服从正态分布N(0,1),若P(ξ>1)=p,则P(-1<ξ<0)=1-p | |
| D. | 在散点图中,回归直线至少经过一个点 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com