
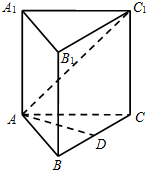
分析 (1)直三棱柱的侧棱和底面垂直,从而可得到AD⊥BB1,并且AD⊥BC,从而由线面垂直的判定定理可得到AD⊥平面BCC1B1;
(2)连接C1D,从而可得到∠AC1D为直线AC1和平面BCC1B1所成角,在Rt△AC1D中,容易求出AD,AC1,从而sin∠AC1D=$\frac{AD}{A{C}_{1}}$.
解答 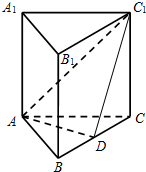 证:(1)直三棱柱ABC-A1B1C1中,BB1⊥面ABC;
证:(1)直三棱柱ABC-A1B1C1中,BB1⊥面ABC;
∴BB1⊥AD,又∵AB=AC,D是BC的中点;
∴AD⊥BC,BC∩BB1=B;
∴AD⊥平面BCC1B1;
(2)连接C1D,由(1)AD⊥平面BCC1B1;
则∠AC1D即为直线AC1与面BCC1B1所成角;
在直角△AC1D中,$AD=\frac{{\sqrt{3}}}{2}$,$A{C_1}=\sqrt{2}$,$sin∠A{C_1}D=\frac{AD}{{A{C_1}}}=\frac{{\sqrt{6}}}{4}$;
即直线AC1与面BCB1C1所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
点评 考查直三棱柱的定义,线面垂直的性质,线面垂直的判定定理,以及线面角的定义,正弦函数的定义.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $-\frac{π}{4}$ | C. | $\frac{3π}{4}$ | D. | 以m的值有关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=cosx | B. | y=|2sinx| | C. | y=cos$\frac{x}{2}$ | D. | y=tanx |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
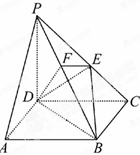 在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.
在四棱柱P-ABCD中,底面ABCD为正方形,PD⊥面ABCD,E是PC的中点,作EF⊥PB交PB于点F,PD=DC.查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com