
分析 (1)由题意利用周期公式可求ω,又由题意当$x=\frac{5}{12}π$时,y=0,结合$0<φ<\frac{π}{2}$可解得φ,再由x=0时,y=1,可求A,从而可求函数解析式.
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,得f(x)单调递增区间,由题意[-m,m]⊆[-$\frac{π}{3}$,$\frac{π}{6}$],解不等式组$\left\{\begin{array}{l}{\stackrel{m≤\frac{π}{6}}{-m≥-\frac{π}{3}}}\\{m>0}\end{array}\right.$,可得m的最大值.
(3)解法1:命题等价于直线y=a,与曲线$g(x)=2sin({2x+\frac{π}{6}})+1$(0$<x<\frac{π}{2}$)有两个交点,当0$<x<\frac{π}{2}$时,可求g(0)=2,$g(\frac{π}{6})=3$,$g(\frac{π}{2})=2$,利用正弦函数的图象可求2<a<3,即可得解;
解法2:设t=2x+$\frac{π}{6}$(0$<x<\frac{π}{2}$),则h(t)=2sint+1,t∈($\frac{π}{6}$,$\frac{7π}{6}$),原命题等价于直线y=a与曲线h(t)=2sint+1,t∈($\frac{π}{6}$,$\frac{7π}{6}$)有两个交点,利用正弦函数的单调性可求实数a的取值范围.
解答 (本题满分为12分)
解:(1)由题意可得函数的周期$T=2({\frac{11}{12}π-\frac{5}{12}π})=π$,
∴ω=2,…(1分)
又由题意当$x=\frac{5}{12}π$时,y=0,得$Asin({2×\frac{5}{12}π+φ})=0$,
结合$0<φ<\frac{π}{2}$可解得$φ=\frac{π}{6}$,…(2分)
再由题意当x=0时,y=1,
∴${A}sin\frac{π}{6}=1$,
∴A=2…(3分)
∴$f(x)=2sin({2x+\frac{π}{6}})$.…(4分)
(2)由2kπ-$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{π}{2}$,k∈Z,得kπ-$\frac{π}{3}$≤x≤kπ+$\frac{π}{6}$,k∈Z,
∴f(x)在区间为:[kπ-$\frac{π}{3}$,kπ+$\frac{π}{6}$],(k∈Z)上是增函数,
∴当k=0时,f(x)在区间[-$\frac{π}{3}$,$\frac{π}{6}$]上是增函数,…(5分)
若函数f(x)在区间[-m,m]上是单调递增函数,则[-m,m]⊆[-$\frac{π}{3}$,$\frac{π}{6}$],…(6分)
∴$\left\{\begin{array}{l}{\stackrel{m≤\frac{π}{6}}{-m≥-\frac{π}{3}}}\\{m>0}\end{array}\right.$,解得0<m≤$\frac{π}{6}$,…(7分)
∴m的最大值是$\frac{π}{6}$,…(8分)
(3)解法1:方程f(x)-a+1=0在区间$(0,\frac{π}{2})$内有两实数根x1,x2(x1<x2)等价于直线y=a,与曲线$g(x)=2sin({2x+\frac{π}{6}})+1$(0$<x<\frac{π}{2}$)有两个交点.…(9分)
∵当0$<x<\frac{π}{2}$时,由(2)知$g(x)=2sin({2x+\frac{π}{6}})+1$在(0,$\frac{π}{6}$]上是增函数,在[$\frac{π}{6}$,$\frac{π}{2}$)上是减函数,…(10分)
且g(0)=2,$g(\frac{π}{6})=2$,$g(\frac{π}{2})=2$.
∴2<a<3,
∴实数a的取值范围是(2,3),…(12分)
解法2:设t=2x+$\frac{π}{6}$(0$<x<\frac{π}{2}$),则h(t)=2sint+1,t∈($\frac{π}{6}$,$\frac{7π}{6}$),
方程f(x)-a+1=0在区间(0,$\frac{π}{2}$)内有两实数根x1,x2(x1<x2)等价于直线y=a与曲线h(t)=2sint+1,t∈($\frac{π}{6}$,$\frac{7π}{6}$)有两个交点.…(9分)
h(t)=2sint+1在($\frac{π}{6}$,$\frac{π}{2}$]上是增函数,在[$\frac{π}{2}$,$\frac{7π}{6}$)上是减函数,…(10分)
$且h(\frac{π}{6})=2$,$h(\frac{π}{2})=2$,$h(\frac{7π}{6})=2$,
∴2<a<3,即实数a的取值范围是(2,3),…12分
点评 本题主要考查了由y=Asin(ωx+φ)的部分图象确定其解析式,正弦函数的图象和性质,不等式的解法及其应用,考查了转化思想和数形结合思想的应用,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x2≥x | |
| B. | 命题“若x=1,则x2=1”的逆命题 | |
| C. | ?α0,β0∈R,使得sin(α0+β0)=sinα0+sinβ0 | |
| D. | 命题“若x≠y,则sinx≠siny”的逆否命题 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
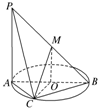 如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:
如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 向左平移$\frac{3π}{4}$个单位长度 | B. | 向右平移$\frac{3π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{3π}{16}$个单位长度 | D. | 向右平移$\frac{3π}{16}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 1+lg99 | D. | 2+lg99 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{9}$ | B. | -$\frac{2}{9}$ | C. | -$\frac{1}{3}$ | D. | -$\frac{7}{18}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com