
分析 (1)假设存在实数a,使f (x)在x=1处取极值,则f′(1)=0,解出a的值,根据x=1的左右均为增函数,则x=1不是极值点.
(2)先对f(x)进行求导,在[2,3]上单调增,则f'(x)≥0在[2,3]上恒成立.求得a的取值范围.
(3)在[1,e]上存在一点x0,使得f(x0)<g(x0)成立,即在[1,e]上存在一点x0,使得h(x0)<0,即函数h(x)=x+$\frac{1+a}{x}-alnx$在[1,e]上的最小值小于零.对h(x)求导.求出h(x)的最小值即可.
解答 解:(1)函数f (x)定义域为(0,+∞),f′(x)=$\frac{a}{x}$+2x-4=$\frac{2{x}^{2}-4x+a}{x}$
假设存在实数a,使f (x)在x=1处取极值,则f′(1)=0,∴a=2,…2分
此时,f′(x)=$\frac{2(x-1)^{2}}{x}$,
∴当0<x<1时,f′(x)>0,f (x)递增;当x>1时,f′(x)>0,f (x)递增.
∴x=1不是f (x)的极值点.
故不存在实数a,使得f (x)在x=1处取极值. …4分
(2)f′(x)=$\frac{2(x-1)^{2}+a-2}{x}$,
①当a≥2时,∴f′(x)≥0,∴f (x)在(0,+∞)上递增,成立; …6分
②当a<2时,令f′(x)>0,则x>1+$\sqrt{\frac{2-a}{2}}$或x<1-$\sqrt{\frac{2-a}{2}}$,
∴f (x)在(1+$\sqrt{\frac{2-a}{2}}$,+∞)上递增,
∵f (x)在[2,3]上存在单调递增区间,∴1+$\sqrt{\frac{2-a}{2}}$<3,解得:-6<a<2
综上,a>-6. …10分
(3)在[1,e]上存在一点x0,使得f(x0)<g(x0)成立,即在[1,e]上存在一点x0,使得h(x0)<0,即函数h(x)=x+$\frac{1+a}{x}-alnx$在[1,e]上的最小值小于零.
$h'(x)-1-\frac{1+a}{{x}^{2}}-\frac{a}{x}=\frac{{x}^{2}-ax-(1+a)}{{x}^{2}}$=$\frac{(x-1)|x-(1+a)|}{{x}^{2}}$,
①当a+1≥e,即a≥e-1时,h(x)在[1,e]上单调递减,
所以h(x)的最小值为q,由h(e)=e+$\frac{1+a}{e}-a<0$可得a>$\frac{{e}^{2}+1}{e-1}$,
因为$\frac{{e}^{2}+1}{e-1}>e-1$,所以a>$\frac{{e}^{2}+1}{e-1}$; …12分
②当a+1≤1,即a≤0时,h(x)在[1,e]上单调递增,
所以h(x)最小值为h(1),由h(1)=1+1+a<0可得a<-2; …14分
③当1<1+a<e,即0<a<e-1时,可得h(x)最小值为h(1+a)=2+a-aln(1+a),
因为0<ln(1+a)<1,所以,0<aln(1+a)<a故h(1+a)=2+a-aln(1+a)>2此时不存在x0使h(x0)<0成立.
综上可得所求a的范围是:$a>\frac{{e}^{2}+1}{e-1}$或a<-2. …16分
解法二:由题意得,存在x∈[1,e],使得a(lnx-$\frac{1}{x}$)>x+$\frac{1}{x}$成立.
令m(x)=lnx-$\frac{1}{x}$,∵m(x)在[1,e]上单调递增,且m(1)=-1<0,m(e)=1-$\frac{1}{e}$>0
故存在x1∈(1,e),使得x∈[1,x1)时,m(x)<0;x∈(x1,e]时,m(x)>0
故存在x∈[1,x1)时,使得a<$\frac{x2+1}{xlnx-1}$成立,…(☆)
或存在x∈(x1,e]时,使得a>$\frac{x2+1}{xlnx-1}$成立,…(☆☆) …12分
记函数F(x)=$\frac{x2+1}{xlnx-1}$,F′(x)=$\frac{(x2-1)lnx-(x+1)2}{(xlnx-1)2}$
当1<x≤e时,(x2-1)lnx-(x+1)2=(x2-1)•$\b\bc\((lnx-\frac{x+1}{x-1})$
∵G(x)=lnx-$\frac{x+1}{x-1}$=lnx-$\frac{2}{x-1}$-1递增,且G(e)=-$\frac{2}{e-1}$<0
∴当1<x≤e时,(x2-1)lnx-(x+1)2<0,即F′(x)<0
∴F(x)在[1,x1)上单调递减,在(x1,e]上也是单调递减,…14分
∴由条件(☆)得:a<F(x)max=F(1)=-2
由条件(☆☆)得:a>F(x)min=F(e)=$\frac{e2+1}{e-1}$
综上可得,a>$\frac{e2+1}{e-1}$或a<-2. …16分.
点评 本题主要考查利用导数解决函数极值问题和利用导数解决函数单调性和参数取值范围,高考常考题型,难度较大.


 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:填空题
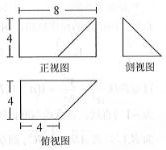 已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.
已知某几何体的三视图如图所示,其正视图为矩形,侧视图为等腰直角三角形,俯视图为直角梯形,则该几何体的体积为$\frac{160}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.
某网络广告A公司计划从甲、乙两个网站选择一个网站拓展广告业务,为此A公司随机抽取了甲、乙两个网站某月中10天的日访问量n(单位:万次),整理后得到如图茎叶图,已知A公司要从网站日访问量的平均值和稳定性两方面进行考量选择.| 选定网站的日访问量n(单位:万次) | A公司的付费标准(单位:元/日) |
| n<25 | 500 |
| 25≤n≤35 | 700 |
| n>35 | 1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 72 | C. | 60 | D. | 120 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
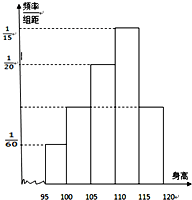 某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率
某幼儿园中班共36个小朋友的身高(单位:厘米)测量结果如下频率查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 408 | B. | 480 | C. | 552 | D. | 816 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com