
分析 根据向量的模长公式与共线定理,得出||$\overrightarrow{a}$|-|$\overrightarrow{b}$||<|$\overrightarrow{a}$-$\overrightarrow{b}$|<|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,从而求出|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围.
解答 解:∵向量|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=3,且$\overrightarrow{a}$与$\overrightarrow{b}$不共线,
∴||$\overrightarrow{a}$|-|$\overrightarrow{b}$||<|$\overrightarrow{a}$-$\overrightarrow{b}$|<|$\overrightarrow{a}$|+|$\overrightarrow{b}$|,
即|2-3|<|$\overrightarrow{a}$-$\overrightarrow{b}$|<2+3,
即1<|$\overrightarrow{a}$-$\overrightarrow{b}$|<5;
∴|$\overrightarrow{a}$-$\overrightarrow{b}$|的取值范围是(1,5).
故答案为:(1,5).
点评 本题考查了平面向量的模长公式与共线定理的应用问题,是基础题目.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{4}$ | B. | 1 | C. | -$\frac{1}{4}$或1 | D. | $\frac{1}{4}$或-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
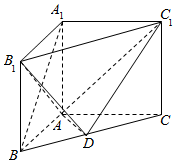 如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.
如图,在直三棱柱ABC-A1B1C1中,点D是BC的中点,AB⊥AC,AB=3,AC=4,AA1=BC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com