
| A. | [$\frac{π}{3}$,π) | B. | ($\frac{π}{6}$,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{2}$) | D. | [$\frac{π}{3}$,$\frac{π}{2}$) |
分析 利用函数的导数,求出导函数,通过导函数值的范围,求解倾斜角的范围.
解答 解:∵f(x)=x3-$\frac{1}{4x}$,
∴f′(x)=3x2+$\frac{1}{4{x}^{2}}$≥2$\sqrt{3{x}^{2}•\frac{1}{4{x}^{2}}}$=$\sqrt{3}$,
点P为函数f(x)=x3-$\frac{1}{4x}$图象上任一点,则过点P的切线的斜率的范围:k≥$\sqrt{3}$.
过点P的切线的倾斜角为α,tanα≥$\sqrt{3}$.
过点P的切线的倾斜角取值范围:[$\frac{π}{3}$,$\frac{π}{2}$).
故选:D.
点评 本题考查直线的斜率与倾斜角的关系,函数的导数的应用,考查计算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
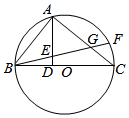 如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.
如图,BC是圆O的直径,点F在弧BC上,点A为劣弧$\widehat{BF}$的中点,作AD⊥BC于点D,BF与AD交于点E,与AC交于点G.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\sqrt{2},2}]$ | B. | $({1,\sqrt{2}}]$ | C. | $({\sqrt{2},+∞})$ | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 第22题 | 第23题 | 第24题 | |
| 甲 | $\frac{1}{6}$ | $\frac{1}{2}$ | $\frac{1}{3}$ |
乙 | $\frac{2}{3}$ | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{5}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{13}{16}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com