Question

19．已知定义域为R的函数f（x）满足f（x）=$\frac{1}{2}$f（x-6），当x∈[0，6]时，f（x）=$\sqrt{3-|x-3|}$，若关于x的方程f（x）=m（x+6）在区间[-6，+∞）内恰有三个不等实根，则实数m的值为（　　）

• A． -$\frac{\sqrt{6}}{12}$
• B． $\frac{\sqrt{6}}{12}$
• C． $\frac{\sqrt{3}}{9}$
• D． 以上均不正确

Answer 1

分析 根据函数f（x）=$\frac{1}{2}$f（x-6），得到f（x）=2f（x+6），作出函数f（x）的图象，利用函数f（x）与g（x）=m（x+6），在区间[-6，+∞）内恰有三个不等实根，建立方程关系进行求解即可．

解答 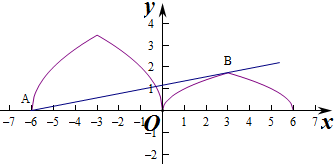解：∵函数f（x）满足f（x）=$\frac{1}{2}$f（x-6），
∴f（x+6）=$\frac{1}{2}$f（x），
即f（x）=2f（x+6），
当x∈[-6，0]时，x+6∈[0，6]，
∵当x∈[0，6]时，f（x）=$\sqrt{3-|x-3|}$，
∴当x∈[-6，0]时，f（x）=2f（x+6）=2$\sqrt{3-|x+6-3|}$=2$\sqrt{3-|x+3|}$，
作出函数f（x）的图象如图：
设g（x）=m（x+6），则g（x）过定点（-6，0），
当x∈[0，3]时，f（x）=$\sqrt{3-|x-3|}$=$\sqrt{x}$，
若g（x）与f（x）=$\sqrt{x}$，相切，设切点（a，b），
则f′（x）=$\frac{1}{2\sqrt{x}}$，则f′（a）=$\frac{1}{2\sqrt{a}}$，
则切线方程为y-b=$\frac{1}{2\sqrt{a}}$（x-a），
即y=$\frac{1}{2\sqrt{a}}$x+$\frac{\sqrt{a}}{2}$，
，当x=-6，y=0时，$\frac{1}{2\sqrt{a}}$×（-6）+$\frac{\sqrt{a}}{2}$=0，
得$\frac{\sqrt{a}}{2}$=$\frac{3}{\sqrt{a}}$，得a=6，即当x∈[0，3]时g（x）与f（x）=$\sqrt{x}$，不可能相切，
则此时当g（x）经过B（3，$\sqrt{3}$）时，g（x）与f（x）有三个交点，
此时g（3）=m（3+6）=9m=$\sqrt{3}$，得m=$\frac{\sqrt{3}}{9}$，
故选：C

点评 本题主要考查函数与方程的应用，根据条件求出函数f（x）的表达式，利用数形结合进行求解是解决本题的关键．综合性较强，有一定的难度．