
分析 由根式内部的代数式大于等于0,分式的分母不为0,列出三个函数所对应的不等式组得答案.
解答 解:(1)由$\left\{\begin{array}{l}{x+1≥0}\\{x≠0}\end{array}\right.$,解得x≥-1且x≠0,
∴f(x)=$\frac{\sqrt{x+1}}{x}$的定义域为[-1,0)∪(0,+∞);
(2)由1-x2≠0,得x≠±1.
∴$f(x)=\frac{1+{x}^{2}}{1-{x}^{2}}$的定义域为(-∞,-1)∪(-1,1)∪(1,+∞);
(3)由$\left\{\begin{array}{l}{x+3≥0}\\{x+2≠0}\end{array}\right.$,解得x≥-3且x≠-2.
∴f(x)=$\sqrt{x+3}$+$\frac{1}{x+2}$的定义域为[-3,-2)∪(-2,+∞).
点评 本题考查函数的定义域及其求法,是基础的计算题.


 全能测控一本好卷系列答案
全能测控一本好卷系列答案科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (1,+∞) | C. | [1,3)∪(3,+∞) | D. | (1,3)∪(3,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若f(x)为增函数,g(x)为增函数,则f(x)+g(x)为增函数 | |
| B. | 若f(x)为减函数,g(x)为减函数,则f(x)+g(x)为减函数 | |
| C. | 若f(x)为增函数,g(x)为减函数,则f(x)+g(x)为增函数 | |
| D. | 若f(x)为减函数,g(x)为增函数,则f(x)-g(x)为减函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
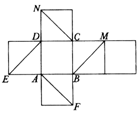 如图是正方体的平面展开图,则在这个正方体中,以下四个判断中,正确的序号是②④.
如图是正方体的平面展开图,则在这个正方体中,以下四个判断中,正确的序号是②④.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{1}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4] | B. | [0,4] | C. | [0,1] | D. | (0,1] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com